Abstract
It is well known that plucking-based frequency up-conversion can enhance the power output in piezoelectric energy harvesting by enabling cyclic free vibration at the fundamental bending mode of the harvester even for very low excitation frequencies. In this work, we present a geometrically nonlinear plucking-based framework for frequency up-conversion in piezoelectric energy harvesting under quasistatic excitations associated with low-frequency stimuli such as walking and similar rigid body motions. Axial shortening of the plectrum is essential to enable plucking excitation, which requires a nonlinear framework relating the plectrum parameters (e.g. overlap length between the plectrum and harvester) to the overall electrical power output. Von Kármán-type geometrically nonlinear deformation of the flexible plectrum cantilever is employed to relate the overlap length between the flexible (nonlinear) plectrum and the stiff (linear) harvester to the transverse quasistatic tip displacement of the plectrum, and thereby the tip load on the linear harvester in each plucking cycle. By combining the nonlinear plectrum mechanics and linear harvester dynamics with two-way electromechanical coupling, the electrical power output is obtained directly in terms of the overlap length. Experimental case studies and validations are presented for various overlap lengths and a set of electrical load resistance values. Further analysis results are reported regarding the combined effects of plectrum thickness and overlap length on the plucking force and harvested power output. The experimentally validated nonlinear plectrum–linear harvester framework proposed herein can be employed to design and optimize frequency up-conversion by properly choosing the plectrum parameters (geometry, material, overlap length, etc) as well as the harvester parameters.
Export citation and abstract BibTeX RIS
1. Introduction
Vibration-based energy harvesting has received dramatically growing attention over the last two decades [1–7]. The main research motivation for this field derives from the reduced power requirement of small electronic components, such as wireless sensor networks used in passive and active monitoring applications. The ultimate goal is to power such small electronic devices by using the vibrational energy available in their environment to reduce or entirely eliminate the burden and maintenance costs of battery replacement. The methods of vibration-to-electric energy conversion include electromagnetic [8, 9], electrostatic [10, 11], and piezoelectric [12–14] transduction techniques, as well as magnetostriction [15, 16], the use of electroactive polymers [17, 18], electret configurations [19, 20], and even gradient effects at submicron thickness levels via flexoelectricity [21, 22]. Among these alternative techniques for vibration-based energy harvesting, piezoelectric transduction has received arguably the most attention for a number of reasons. The main advantages of piezoelectric materials in energy harvesting are their large power density and ease of application. Voltage outputs in electromagnetic energy harvesting are typically very low and often multi-stage post-processing is required in order to reach a voltage level that can charge a storage component. In piezoelectric energy harvesting, however, usable voltage outputs can be obtained directly from the piezoelectric material itself. In electrostatic energy harvesting, an input voltage or charge needs to be applied so that the relative vibratory motion of the capacitor elements creates an alternating electrical output. The voltage response in piezoelectric energy harvesting emerges from the constitutive behavior of the material, which eliminates the requirement of an external voltage input. As another advantage, piezoelectric devices can be fabricated in micro-scale, owing to the well-established thick-film and thin-film fabrication techniques [5]. Various piezoelectric energy harvester configurations and models have been developed, including both linear [12–14] and nonlinear [23–26] ones.
Several ambient vibration/motion energy harvesting problems of potential industrial impact contain mechanical energy at very low frequencies (∼ a few Hz). For instance, energy harvesting from human walking for wearable electronics is of great interest in the domain of the Internet of Things for numerous applications, ranging from self-powered on-body health monitoring systems to smart shoes for fitness tracking. Various research groups explored human motion energy harvesting using piezoelectric transduction, mostly by directly inserting piezoelectric elements and cantilevers to exploit shoe slow deformation or to directly excite cantilever configurations due to acceleration fluctuations at the heel [27–30]. Normally, designing a piezoelectric energy harvester that would resonate at such low frequencies would require impractically large dimensions and/or proof mass. One approach to alleviate this issue is to enable frequency up-conversion via a plucking mechanism as explored by Pozzi and Zhu [31, 32] in their knee-joint energy harvester design (we note that others suggested magnetic plucking [33–36], impact mechanisms [37, 38], and nonlinear secondary resonances [39, 40] for frequency up-conversion). The idea of plucking-based frequency up-conversion relies on the quasistatic initial displacement excitation of a cantilevered energy harvester in a cyclic way via a flexible plectrum (figure 1) so that the harvester responds in free vibration at its fundamental natural frequency at each plucking cycle (details of the concept can be found in [31]). Therefore, this concept requires a flexible plectrum with a nonlinear deformation that results in significant (finite—i.e. not infinitesimal) axial shortening at the instant of release for plucking excitation, although previous work avoided nonlinear plectrum mechanics and/or the plectrum as a design component entirely. A complete model can enable optimization of the entire system, including the plectrum, its overlap length, thickness, material, among other parameters. A plausible approach is to combine a geometrically nonlinear plectrum model with a linear piezoelectric energy harvester model for the complete picture to relate the overlap length between the plectrum and the harvester to the power output, as explored in the present work.
Figure 1. (a) Schematic of plucking-based frequency up-conversion mechanism using a geometrically nonlinear (flexible) plectrum and a linear (stiff) bimorph piezoelectric energy harvester and (b) relevant geometric parameters (the release height h is related to the overlap length d and the plectrum length L via geometrically nonlinear deformation of the plectrum cantilever).
Download figure:
Standard image High-resolution imageIn the following, first we derive the quasistatic nonlinear deflection of a flexible plectrum based on the von Kármán theory to relate the overlap length to the release height in an effort to identify the transverse quasistatic tip force transmitted to the harvester, and then briefly review the linearized piezoelectric energy harvester model that takes the initial displacement of the harvester due to the transmitted force as the input. Experimental validations are then presented for a bimorph piezoelectric energy harvester combined with a flexible plectrum for a range of overlap lengths and load resistance values. Further numerical simulations are presented to explore the effects of various parameters such as the combined effects of the plectrum thickness and overlap length on the transmitted force and harvested power.
2. Model development for nonlinear plectrum and linear harvester combination
The plucking-based frequency up-conversion process is summarized in figure 1 for a geometrically nonlinear plectrum and a linear piezoelectric energy harvester combination. It is assumed that the bimorph harvester is relatively stiff and undergoes small oscillations, while the plectrum exhibits large deformations (which is necessary to achieve plucking excitation—i.e. axial shortening associated with bending deformation, making the overlap length d and the release height h in figure 1 critical geometric parameters). This section first presents a quasistatic geometrically nonlinear model based on the von Kármán theory to relate the vertical tip displacement of the plectrum to its overlap length with the harvester in an effort to identify the transverse tip force, and hence the initial tip displacement of the relatively stiff (linear) harvester in each quasistatic plucking motion. Then, the initial displacement condition resulting from the tip force is employed in a geometrically and materially linear cantilevered bimorph harvester model to simulate free vibrations resulting from the plucking, as described in the following.
2.1. Nonlinear plectrum deflection based on the von Kármán theory
The overall goal in this section is to obtain a relation between the overlap length d and the release height h for a given plectrum length L. To this end, it is required to implement a geometrically nonlinear model for the quasistatic flexible plectrum deformation. The homogeneous differential equations governing the static deflection of a thin cantilever (flexible plectrum in figure 1) with von Kármán-type geometric nonlinearity [41] can be given by
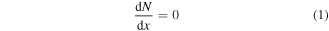
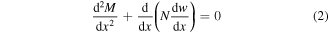
where the resultant axial force (N) and the bending moment (M) terms are
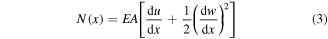
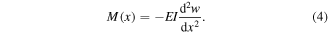
Here, u and w are the longitudinal and transverse displacement variables (as shown in figure 1(b)), respectively, EA is the axial rigidity and EI is the flexural rigidity of the plectrum.
The resultant transverse shear force term can be extracted from equation (2) as
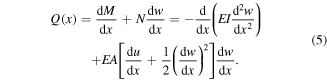
Next, we introduce the quasistatic tip force that is associated with the plucking excitation at the instant of release depicted in figure 1(b). For the clamped-free plectrum beam with a transversely applied force (P) at the free end, the boundary conditions at the clamped 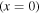 and the free
and the free 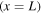 ends are
ends are
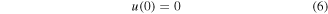
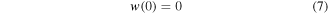
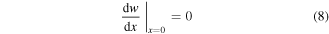
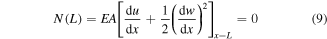
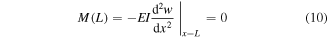
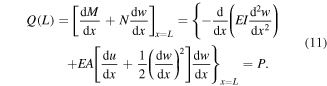
It should be noted that this quasistatic transverse tip force at the instant of the release is the same tip force acting on the harvester (in the opposite direction) that yields the initial displacement for each plucking motion.
From equation (1), the resultant axial force is constant 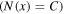 throughout the plectrum, but from the boundary condition given by equation (9),
throughout the plectrum, but from the boundary condition given by equation (9),  Thus,
Thus,  throughout the length and it follows from equation (3) that
throughout the length and it follows from equation (3) that
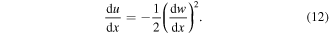
Using equation (12) along with the boundary condition given by equation (6),

Using equation (12) and in view of the fixed flexural rigidity (EI) of the uniform plectrum, equation (11) reduces to
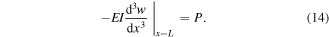
From the boundary conditions defined by equations (7), (8), (10) and (14), the transverse deflection in terms of the applied force can be obtained as
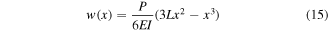
yielding
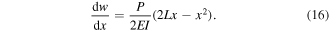
Substituting equation (16) into equation (13) gives
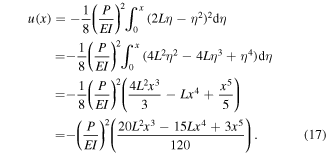
From equation (15),
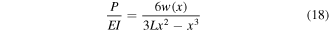
which can be substituted into equation (17) to give
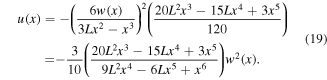
Equation (19) relates the longitudinal deflection 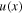 of the plectrum neutral axis to its geometrically large transverse deflection
of the plectrum neutral axis to its geometrically large transverse deflection  Therefore, at the free end of the plectrum, the axial deflection due to transverse deflection can be given by
Therefore, at the free end of the plectrum, the axial deflection due to transverse deflection can be given by
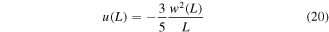
where, expectedly,  regardless of the sign of
regardless of the sign of 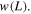
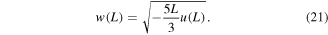
Hence, if the overlap length of the plectrum on the stiff harvester beam is given by d, then its tip deflection at the instant of release (i.e. the release height in figure 1) is
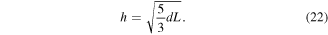
Note that the transverse tip force P at the instant of release can be obtained via equation (22) by setting  and
and 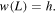
2.2. Linear piezoelectric energy harvester excited by the nonlinear plectrum
Since the bimorph harvester is much stiffer than the plectrum exciting it (a reasonable underlying assumption), the harvester behavior is approximated by the linear cantilevered bimorph piezoelectric energy harvester model of Erturk and Inman [6, 14]. Note that under large stress fields (i.e. very hard excitation of the harvester by the plectrum due to larger overlap length, plectrum thickness, or elastic modulus, etc), material nonlinearities could be pronounced even for a stiff and geometrically linear piezoelectric bimorph, and those nonlinearities can be accommodated as needed using a materially nonlinear framework [42] (which is beyond the scope of the current work).
In view of the tip deflection-based deformation shape (predominantly in the first bending vibration mode), assuming a single-mode solution for the vibration response yields the following approximation:
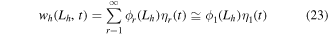
where 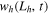 is the transverse displacement of the bimorph harvester (of overhang length
is the transverse displacement of the bimorph harvester (of overhang length 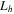 ),
), 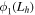 is the mass normalized eigenfunction (based on the Euler–Bernoulli theory) evaluated at the cantilever tip, and
is the mass normalized eigenfunction (based on the Euler–Bernoulli theory) evaluated at the cantilever tip, and  is the modal coordinate. Then, the governing electromechanical equations for free vibrations are:
is the modal coordinate. Then, the governing electromechanical equations for free vibrations are:
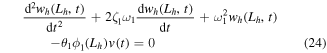
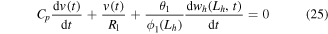
where 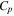 is the equivalent capacitance of the bimorph,
is the equivalent capacitance of the bimorph,  is the load resistance,
is the load resistance, 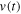 is the voltage across the resistance,
is the voltage across the resistance, 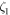 is the viscous damping ratio,
is the viscous damping ratio, 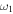 is the natural frequency of the linear bimorph harvester for the first bending mode in short circuit, and
is the natural frequency of the linear bimorph harvester for the first bending mode in short circuit, and 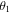 is the modal electromechanical coupling that depends on the cross-section and material parameters of the bimorph [6, 14]. The initial conditions due to quasistatic plucking excitation are
is the modal electromechanical coupling that depends on the cross-section and material parameters of the bimorph [6, 14]. The initial conditions due to quasistatic plucking excitation are

Here, 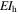 is the flexural rigidity of the bimorph harvester and
is the flexural rigidity of the bimorph harvester and 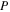 is the quasistatic transverse tip force on the harvester due to the plucking deflection h in figure 1, which is the same as the tip force of the plectrum under quasistatic conditions:
is the quasistatic transverse tip force on the harvester due to the plucking deflection h in figure 1, which is the same as the tip force of the plectrum under quasistatic conditions:
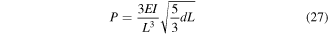
where EI is the flexural rigidity of the plectrum as in the derivation given in the previous section.
Equations (24) and (25) can then be cast into first-order form and simulated in time domain using the initial conditions given by equation (26). Note that an implicit assumption is that the quasistatic external stimulus on the plectrum (due to walking, etc) is large enough to enable plucking excitation, which can easily be checked by comparing the external load on the plectrum to the load at the release given by equation (27).
3. Experimental validation and effect of various parameters
In this section, first a bimorph piezoelectric energy harvester is experimentally tested and modeled for its fundamental bending vibration mode under base excitation to ensure that the model parameters are accurate. Then, the plectrum setup is employed for various overlap lengths and a range of electrical load resistance values for model validation. Finally, additional simulations are performed in an effort to understand the effects of various parameters on the harvested power.
3.1. Linear bimorph harvester and its frequency response
The bimorph harvester used in the experiments (Piezo Systems, Inc.—T215-H4-503X) is shown in figure 2(a) along with its experimental setup. This base excitation setup is employed to ensure that the parameters in the bimorph energy harvester model are accurate prior to the plucking experiments, and to identify or update parameters such as the mechanical damping ratio (in short circuit) and static capacitance. The resulting fundamental short-circuit resonance frequency of the harvester is around 74.6 Hz, which becomes 78.8 Hz in open circuit as observed in figures 2(b) and (c). The voltage and vibration frequency response function (FRF) simulations are shown for a range of resistive electrical loads, revealing very good agreement with the experimental data. Therefore, bimorph harvester parameters based on the model in [6, 14] can be combined with the nonlinear plectrum model to simulate the plucking experiments performed next.
Figure 2. (a) Experimental setup and a close-up view of the bimorph harvester on the shaker for harvester model validation and parameter identification prior to the plucking experiments; (b) voltage FRFs and (c) tip velocity FRFs (per base acceleration) for a wide range of load resistance values (solids lines are model simulations and dots are experimental data).
Download figure:
Standard image High-resolution image3.2. Nonlinear plectrum–linear harvester combination and model validation
The experimental setup for plucking-based energy harvesting is shown in figure 3(a) and a close-up of the plucking excitation is given in figure 3(b). The plectrum is made of stainless steel and it has a thickness of around 0.05 mm (much thinner than the bimorph harvester), overhang length of 45 mm, and its width of 31.8 mm is identical to that of the harvester. As can be seen from figure 3, the plectrum deformation can be quite nonlinear (which is necessary for the release and plucking to take place). Simulations of the voltage output and the tip velocity of the harvester obtained using the combined nonlinear plectrum–linear harvester model are shown in figure 4 for two select overlap lengths (2 and 10 mm—which are the two extremes considered here). The load resistance in figure 4 is the optimal value (20 kΩ) among the set of resistors used in the experiments. Overall, the voltage and tip velocity time series of the harvester shown in figure 4 reveal very good agreement between the model simulations and experimental measurements.
Figure 3. (a) Experimental setup showing the bimorph harvester and the plectrum; (b) close-up views of the linear (stiff) harvester and nonlinear (flexible) plectrum showing geometrically nonlinear deformation of the plectrum, while the harvester deformation is geometrically linear.
Download figure:
Standard image High-resolution imageFigure 4. Voltage and tip velocity time histories associated with plucking excitation for the optimal load resistance of 20 kΩ and two extreme overlap lengths explored: (a) 2 mm and (b) 10 mm (model simulations and experimental data).
Download figure:
Standard image High-resolution imageNext, the average electrical power delivered to the resistive load is analyzed by using the time series of the harvester response under plucking excitation for a range of load resistance values. Note that the root-mean-square voltage and the average power are easily calculated using the voltage time series (such as those in figure 4) for a time window that covers until the oscillations die out for a given load resistance. For a given plectrum and harvester combination, the main input to the nonlinear plectrum and linear harvester combination is the overlap length d. We recall that a critical aspect of the problem is the relationship between the geometric parameters d (overlap length) and h (released height), as shown in figure 1. As can be anticipated, the overlap length (d) between the plectrum and the harvester alters the amount of force on the harvester (discussed further in the next section), and therefore affects the harvested power output, as shown in figure 5. The overall results are shown in this figure for various load resistance and overlap length values, where the model simulations (solid lines) agree well with the experimental data points. Note that a significant part of the mismatch is due to the difficulty in achieving zero initial velocity condition in the experiments.
Figure 5. (a) Average power versus load resistance for different overlap lengths; (b) average power at the optimal load resistance versus overlap length (model simulations and experimental data).
Download figure:
Standard image High-resolution image3.3. Effects of various system parameters
Having validated the electromechanical model, the effects of critical system parameters, such as the plectrum thickness and overlap length, on the tip force and deflection as well as the harvested power are simulated for the same system shown in figure 3. First, the quasistatic transverse tip force transmitted to the harvester at the instant of the release and the resulting harvester tip displacement are simulated as a function of plectrum thickness and overlap length. As expected, it is observed from figure 6 that the tip displacement and force follow similar trends when the plectrum thickness and overlap length are changed. The maximum harvester tip deflection of 0.44 mm and tip force of 0.21 N are seen when the plectrum thickness and overlap are at their maximum simulated values among the parameter ranges in figure 6. Either the plectrum thickness (in design) or the overlap length can be increased in order to increase the force transmitted to the harvester. It is important to note that, in these simulations, the tip displacement of the harvester does not exceed a value that would result in the failure of the harvester (which can easily be shown by analyzing the maximum stress at the root), which would be a typical design constraint.
Figure 6. Variation of (a) the tip force and (b) the tip displacement of the harvester with plectrum thickness and overlap length.
Download figure:
Standard image High-resolution imageIncreasing the overlap length and plectrum thickness increases the average power output from the harvester. Figures 7(a) and (b) show the average power variation with plectrum thickness at the two extreme cases of overlap length (2 and 10 mm). This effect can be seen for all overlap lengths in figure 8(a). The average power at optimal load increases by almost four orders of magnitude (from 0.15 to 108 μW) as the overlap length is increased from 2 to 10 mm, which can be seen in figure 8(b). From the design and application standpoint, for a given plectrum thickness, one can increase the overlap length to increase the power output. Alternatively, the plectrum thickness can be tailored to increase the power output under the constraint of a fixed overlap length. The effects of several other parameters, such as the plectrum material (i.e. elastic modulus), can be simulated using the proposed model in order to optimize the harvested power, while avoiding a mechanical failure in the harvester.
Figure 7. Average power output versus plectrum thickness and load resistance for (a) 2 mm and (b) 10 mm overlap length.
Download figure:
Standard image High-resolution imageFigure 8. (a) Average power output for all simulated overlap lengths versus plectrum thickness and load resistance; (b) optimal power output (at 20 kΩ) versus plectrum thickness for all overlap lengths.
Download figure:
Standard image High-resolution image4. Conclusions
Several vibration energy harvesting problems involve motion at very low frequencies (∼ a few Hz), such as the harvesting of walking energy for wearable electronics, which would require impractically large harvester dimensions to enable resonant response. It is well known that plucking-based frequency up-conversion is a popular solution to alleviate this issue by exciting the harvester to respond in free vibration at its natural frequency. In this work, a geometrically nonlinear plucking-based electromechanical modeling framework is presented and experimentally validated for frequency up-conversion in piezoelectric energy harvesting under quasistatic excitations. Axial shortening of the plectrum enables plucking excitation, which requires a nonlinear framework in modeling. We employ von Kármán-type geometrically nonlinear deformation of the flexible plectrum cantilever to relate the overlap length between the flexible (nonlinear) plectrum and the stiff (linear) harvester in order to estimate the force transmitted to the harvester. Nonlinear plectrum mechanics and linear harvester dynamics are combined to obtain the voltage response time series (and thereby the average power output) and the vibration response time series directly in terms of the overlap length. Experimental case studies and validations are presented for various overlap lengths and a set of electrical load resistance values. Additional results are presented pertaining to the combined effects of the plectrum thickness and overlap length on the plucking force and harvested power output. The experimentally validated nonlinear plectrum–linear harvester framework proposed in this work can be used to properly choose the plectrum parameters (geometry, material, etc), as well as the harvester parameters and the overlap length to maximize the power output, while ensuring that the harvester does not fail under large displacements and stresses. Note that the proposed framework can easily by combined with a materially nonlinear harvester model, such as the one in [42].
Acknowledgments
We would like to acknowledge the project sponsors at Delaware North Corporation (DNC), NASA's Kennedy Space Center (KSC), the Wells Fargo Foundation, and the National Science Foundation grant CMMI 1254262. We would also like to thank the Woodruff School of Mechanical Engineering at Georgia Tech and ATAS laboratories at GTRI for the support to ensure the success of this program.









