Lagrangian mechanics

Lagrangian mechanics is a re-formulation of classical mechanics using the principle of stationary action (also called the principle of least action). It is not as general as the principle of stationary action because it is restricted to equilibrium problems. Lagrangian mechanics applies to systems whether or not they conserve energy or momentum, and it provides conditions under which energy, momentum or both are conserved. It was introduced by the Italian-French mathematician Joseph-Louis Lagrange in 1788.

In Lagrangian mechanics, the trajectory of a system of particles is derived by solving the Lagrange equations in one of two forms, either the Lagrange equations of the first kind, which treat constraints explicitly as extra equations, often using Lagrange multipliers; or the Lagrange equations of the second kind, which incorporate the constraints directly by judicious choice of generalized coordinates. The fundamental lemma of the calculus of variations shows that solving the Lagrange equations is equivalent to finding the path for which the action functional is stationary, a quantity that is the integral of the Lagrangian over time.

The use of generalized coordinates may considerably simplify a system's analysis. For example, consider a small frictionless bead traveling in a groove. If one is tracking the bead as a particle, calculation of the motion of the bead using Newtonian mechanics would require solving for the time-varying constraint force required to keep the bead in the groove. For the same problem using Lagrangian mechanics, one looks at the path of the groove and chooses a set of independent generalized coordinates that completely characterize the possible motion of the bead. This choice eliminates the need for the constraint force to enter into the resultant system of equations. There are fewer equations since one is not directly calculating the influence of the groove on the bead at a given moment.

Lagrangian mechanics ability to work in generalized coordinate systems makes it suitable for use in special relativity which coordinate systems change for different observers. It is used as the standard language of particle physics to express the standard model in terms of Lagrangians.

The Lagrangian, L, of a dynamical system is a mathematical function that summarizes the dynamics of the system. For a simple mechanical system, it is the value given by the kinetic energy of the particle minus the potential energy of the particle but it may be generalized to more complex systems. It is used primarily as a key component in the Euler-Lagrange equations to find the path of a particle according to the principle of least action.

The Lagrangian is named after Italian mathematician and astronomer Joseph Louis Lagrange. The concept of a Lagrangian was introduced in a reformulation of classical mechanics introduced by Lagrange known as Lagrangian mechanics in 1788. This reformulation was needed in order to explore mechanics in alternative systems to Cartesian coordinates such as polar, cylindrical and spherical coordinates, and where the coordinates do not necessarily refer to position, for which Newton's formulation of classical mechanics is not convenient.

The Lagrangian has since been used in a method to find the acceleration of a particle in a Newtonian gravitational field and to derive the Einstein field equations. This led to its use in applying electromagnetism to curved spacetime and in describing charged black holes. It also has additional uses in Mathematical formalism to find the functional derivative of an action, and in engineering for the analysis and optimisation of dynamic systems.

Conceptual framework

Generalized coordinates

For one particle acted on by external forces, Newton's second law forms a set of 3 second-order ordinary differential equations, one for each dimension. Therefore, the motion of the particle can be completely described by 6 independent variables: 3 initial position coordinates and 3 initial velocity coordinates. Given these, the general solutions to Newton's second law become particular solutions that determine the time evolution of the particle's behaviour after its initial state (t = 0).

The most familiar set of variables for position r = (r₁, r₂, r₃) and velocity $\mathbf {\dot {r}} _{j}=({\dot {r}}_{1},{\dot {r}}_{2},{\dot {r}}_{3})$ are Cartesian coordinates and their time derivatives (i.e. position (x, y, z) and velocity (v_x, v_y, v_z) components). Determining forces in terms of standard coordinates can be complicated, and usually requires much labour.

An alternative and more efficient approach is to use only as many coordinates as are needed to define the position of the particle, at the same time incorporating the constraints on the system, and writing down kinetic and potential energies. In other words, to determine the number of degrees of freedom the particle has, i.e. the number of possible ways the system can move subject to the constraints (forces that prevent it moving in certain paths). Energies are much easier to write down and calculate than forces, since energy is a scalar while forces are vectors.

These coordinates are generalized coordinates, denoted $q_{j}$, and there is one for each degree of freedom. Their corresponding time derivatives are the generalized velocities, ${\dot {q_{j}}}$. The number of degrees of freedom is usually not equal to the number of spatial dimensions: multi-body systems in 3-dimensional space (such as Barton's Pendulums, planets in the solar system, or atoms in molecules) can have many more degrees of freedom incorporating rotations as well as translations. This contrasts the number of spatial coordinates used with Newton's laws above.

The position vector r in a standard coordinate system (like Cartesian, spherical etc.), is related to the generalized coordinates by some transformation equation:

${\mathbf {r}}={\mathbf {r}}(q_{i},t).\,$

where there are as many q_i as needed (number of degrees of freedom in the system). Likewise for velocity and generalized velocities.

For example, for a simple pendulum of length ℓ, there is the constraint of the pendulum bob's suspension (rod/wire/string etc.). The position r depends on the x and y coordinates at time t, that is, r(t)=(x(t),y(t)), however x and y are coupled to each other in a constraint equation (if x changes y must change, and vice versa). A logical choice for a generalized coordinate is the angle of the pendulum from vertical, θ, so we have r = (x(θ), y(θ)) = r(θ), in which θ = θ(t). Then the transformation equation would be

${\mathbf {r}}(\theta (t))=(\ell \sin \theta ,-\ell \cos \theta )$

and so

${\mathbf {\dot {r}}}(\theta (t),{\dot {\theta }}(t))=(\ell \,{\dot {\theta }}\cos \theta ,\ell \,{\dot {\theta }}\sin \theta )$

which corresponds to the one degree of freedom the pendulum has. The term "generalized coordinates" is really a holdover from the period when Cartesian coordinates were the default coordinate system.

In general, from m independent generalized coordinates q_j, the following transformation equations hold for a system composed of n particles:

${\begin{array}{r c l}\mathbf {r} _{1}&=&\mathbf {r} _{1}(q_{1},q_{2},\cdots ,q_{m},t)\\\mathbf {r} _{2}&=&\mathbf {r} _{2}(q_{1},q_{2},\cdots ,q_{m},t)\\&\vdots &\\\mathbf {r} _{n}&=&\mathbf {r} _{n}(q_{1},q_{2},\cdots ,q_{m},t)\end{array}}$

where m indicates the total number of generalized coordinates. An expression for the virtual displacement (infinitesimal), δr_i of the system for time-independent constraints or "velocity-dependent constraints" is the same form as a total differential

$\delta \mathbf {r} _{i}=\sum _{j=1}^{m}{\frac {\partial \mathbf {r} _{i}}{\partial q_{j}}}\delta q_{j},$

where j is an integer label corresponding to a generalized coordinate.

The generalized coordinates form a discrete set of variables that define the configuration of a system. The continuum analogue for defining a field are field variables, say ϕ(r, t), which represents density function varying with position and time.

D'Alembert's principle and generalized forces

D'Alembert's principle introduces the concept of virtual work due to applied forces F_i and inertial forces, acting on a three-dimensional accelerating system of n particles whose motion is consistent with its constraints,

Mathematically, the virtual work δW done on a particle of mass m_i through a virtual displacement δr_i (consistent with the constraints) is:

D'Alembert's principle

$\delta W=\sum _{i=1}^{n}(\mathbf {F} _{i}-m_{i}\mathbf {a} _{i})\cdot \delta \mathbf {r} _{i}=0.$

where a_i are the accelerations of the particles in the system and i = 1, 2,...,n simply labels the particles. In terms of generalized coordinates

$\delta W=\sum _{j=1}^{m}\sum _{i=1}^{n}(\mathbf {F} _{i}-m_{i}\mathbf {a} _{i})\cdot {\frac {\partial \mathbf {r} _{i}}{\partial q_{j}}}\delta q_{j}=0.$

this expression suggests that the applied forces may be expressed as generalized forces, Q_j. Dividing by δq_j gives the definition of a generalized force:

$Q_{j}={\frac {\delta W}{\delta q_{j}}}=\sum _{i=1}^{n}\mathbf {F} _{i}\cdot {\frac {\partial \mathbf {r} _{i}}{\partial q_{j}}}.$

If the forces F_i are conservative, there is a scalar potential field V in which the gradient of V is the force:

$\mathbf {F} _{i}=-\nabla V\Rightarrow Q_{j}=-\sum _{i=1}^{n}\nabla V\cdot {\frac {\partial \mathbf {r} _{i}}{\partial q_{j}}}=-{\frac {\partial V}{\partial q_{j}}}.$

i.e. generalized forces can be reduced to a potential gradient in terms of generalized coordinates. The previous result may be easier to see by recognizing that V is a function of the r_i, which are in turn functions of q_j, and then applying the chain rule to the derivative of $V$ with respect to q_j.

Kinetic energy relations

The kinetic energy, T, for the system of particles is defined by

$T={\frac {1}{2}}\sum _{i=1}^{n}m_{i}\mathbf {\dot {r}} _{i}\cdot \mathbf {\dot {r}} _{i}.$

In terms of the kinetic energy, the equations of motion in a set of generalized coordinates can be written:

Generalized equations of motion

$Q_{j}={\frac {\mathrm {d} }{\mathrm {d} t}}\left({\frac {\partial T}{\partial {\dot {q}}_{j}}}\right)-{\frac {\partial T}{\partial q_{j}}}$

Newton's laws are contained in it, yet there is no need to find the constraint forces because virtual work and generalized coordinates (which account for constraints) are used. This equation in itself is not actually used in practice, but is a step towards deriving Lagrange's equations (see below).

Derivation of the generalized equations of motion

The partial derivatives of T with respect to the generalized coordinates qj and generalized velocities ${\dot {q}}_{j}$ are: ${\frac {\partial T}{\partial q_{j}}}=\sum _{i=1}^{n}m_{i}\mathbf {\dot {r}} _{i}\cdot {\frac {\partial \mathbf {\dot {r}} _{i}}{\partial q_{j}}}$ $\quad {\frac {\partial T}{\partial {\dot {q}}_{j}}}=\sum _{i=1}^{n}m_{i}\mathbf {\dot {r}} _{i}\cdot {\frac {\partial \mathbf {\dot {r}} _{i}}{\partial {\dot {q}}_{j}}}.$ it can be shown that ${\frac {\partial \mathbf {\dot {r}} _{i}}{\partial {\dot {q_{j}}}}}={\frac {\partial \mathbf {r} _{i}}{\partial q_{j}}}.$ Then: $\quad {\frac {\partial T}{\partial {\dot {q}}_{j}}}=\sum _{i=1}^{n}m_{i}\mathbf {\dot {r}} _{i}\cdot {\frac {\partial \mathbf {r} _{i}}{\partial q_{j}}}\ .$ The total time derivative of this equation is ${\frac {\mathrm {d} }{\mathrm {d} t}}{\frac {\partial T}{\partial {\dot {q}}_{j}}}=\sum _{i=1}^{n}m_{i}\mathbf {\ddot {r}} _{i}\cdot {\frac {\partial \mathbf {r} _{i}}{\partial q_{j}}}+\sum _{i=1}^{n}m_{i}\mathbf {\dot {r}} _{i}\cdot {\frac {\partial \mathbf {\dot {r}} _{i}}{\partial q_{j}}}=Q_{j}+{\frac {\partial T}{\partial q_{j}}}\ .$ resulting in the generalized equations of motion.

Lagrangian and action

The core element of Lagrangian mechanics is the Lagrangian function, which summarizes the dynamics of the entire system in a very simple expression. The physics of analyzing a system is reduced to choosing the most convenient set of generalized coordinates, determining the kinetic and potential energies of the constituents of the system, then writing down the equation for the Lagrangian to use in Lagrange's equations. It is defined by

$L=T-V\,$

where T is the total kinetic energy and V is the total potential energy of the system.

The next fundamental element is the action ${\mathcal {S}}$, defined as the time integral of the Lagrangian:

${\mathcal {S}}=\int _{t_{1}}^{t_{2}}L\,\mathrm {d} t.$

This also contains the dynamics of the system, and has deep theoretical implications (discussed below). Technically, the action is a functional, that is, it is a function that maps the full Lagrangian function for all times between t₁ and t₂ to a scalar value for the action. Its dimensions are the same as angular momentum.

In classical field theory, the physical system is not a set of discrete particles, but rather a continuous field defined over a region of 3d space. Associated with the field is a Lagrangian density ${\mathcal {L}}(\mathbf {r} ,t)$ defined in terms of the field and its derivatives at a location $\mathbf {r}$. The total Lagrangian is then the integral of the Lagrangian density over 3d space (see volume integral):

$L(t)=\int {\mathcal {L}}(\mathbf {r} ,t)\mathrm {d} ^{3}\mathbf {r} \,$

where d³r is a 3d differential volume element, must be used instead. The action becomes an integral over space and time:

${\mathcal {S}}=\int _{t_{1}}^{t_{2}}\int {\mathcal {L}}(\mathbf {r} ,t)\mathrm {d} ^{3}\mathbf {r} \mathrm {d} t.$

Hamilton's principle of stationary action

Let q₀ and q₁ be the coordinates at respective initial and final times t₀ and t₁. Using the calculus of variations, it can be shown that Lagrange's equations are equivalent to Hamilton's principle:

The trajectory of the system between t₀ and t₁ has a stationary action S.

By stationary, we mean that the action does not vary to first-order from infinitesimal deformations of the trajectory, with the end-points (q₀, t₀) and (q₁,t₁) fixed. Hamilton's principle can be written as:

$\delta {\mathcal {S}}=0.\,\!$

Thus, instead of thinking about particles accelerating in response to applied forces, one might think of them picking out the path with a stationary action.

Hamilton's principle is sometimes referred to as the principle of least action, however the action functional need only be stationary, not necessarily a maximum or a minimum value. Any variation of the functional gives an increase in the functional integral of the action.

We can use this principle instead of Newton's Laws as the fundamental principle of mechanics, this allows us to use an integral principle (Newton's Laws are based on differential equations so they are a differential principle) as the basis for mechanics. However it is not widely stated that Hamilton's principle is a variational principle only with holonomic constraints, if we are dealing with nonholonomic systems then the variational principle should be replaced with one involving d'Alembert principle of virtual work. Working only with holonomic constraints is the price we have to pay for using an elegant variational formulation of mechanics.

Illustration

The trajectory of a thrown ball is characterized by the sum of the Lagrangian values at each time being a (local) minimum.

The Lagrangian L can be calculated at several instants of time t, and a graph of L against t can be drawn. The area under the curve is the action. Any different path between the initial and final positions leads to a larger action than that chosen by nature. Nature chooses the smallest action – this is the Principle of Least Action.

If Nature has defined the mechanics problem of the thrown ball in so elegant a fashion, might She have defined other problems similarly. So it seems now. Indeed, at the present time it appears that we can describe all the fundamental forces in terms of a Lagrangian. The search for Nature's One Equation, which rules all of the universe, has been largely a search for an adequate Lagrangian.

— Robert Adair, The Great Design: Particles, Fields, and Creation

Using only the principle of least action and the Lagrangian we can deduce the correct trajectory, by trial and error or the calculus of variations.

Lagrange's equations of the first kind

Lagrange introduced an analytical method for finding stationary points using the method of Lagrange multipliers, and also applied it to mechanics.

For a system subject to the (holonomic) constraint equation on the generalized coordinates:

$F(r_{1},r_{2},r_{3})=A$

where A is a constant, then Lagrange's equations of the first kind are:

$\left[{\frac {\partial L}{\partial r_{j}}}-{\frac {\mathrm {d} }{\mathrm {d} t}}\left({\frac {\partial L}{\partial {\dot {r}}_{j}}}\right)\right]+\lambda {\frac {\partial F}{\partial r_{j}}}=0$

where λ is the Lagrange multiplier. By analogy with the mathematical procedure, we can write:

${\frac {\delta L}{\delta r_{j}}}+\lambda {\frac {\partial F}{\partial r_{j}}}=0$

where

${\frac {\delta L}{\delta r_{j}}}={\frac {\partial L}{\partial r_{j}}}-{\frac {\mathrm {d} }{\mathrm {d} t}}\left({\frac {\partial L}{\partial {\dot {r}}_{j}}}\right)$

denotes the variational derivative.

For e constraint equations F₁, F₂,..., F_e, there is a Lagrange multiplier for each constraint equation, and Lagrange's equations of the first kind generalize to:

Lagrange's equations (1st kind)

${\frac {\delta L}{\delta r_{j}}}+\sum _{i=1}^{e}\lambda _{i}{\frac {\partial F_{i}}{\partial r_{j}}}=0$

This procedure does increase the number of equations, but there are enough to solve for all of the multipliers. The number of equations generated is the number of constraint equations plus the number of coordinates, i.e. e + m. The advantage of the method is that (potentially complicated) substitution and elimination of variables linked by constraint equations can be bypassed.

There is a connection between the constraint equations F_j and the constraint forces N_j acting in the conservative system (forces are conservative):

$N_{j}=\sum _{i=1}^{e}\lambda _{i}{\frac {\partial F_{i}}{\partial r_{j}}}$

which is derived below.

Derivation of connection between constraint equations and forces

The generalized constraint forces are given by (using the definition of generalized force above): $N_{j}=\sum _{i=1}^{n}\mathbf {N} _{i}\cdot {\frac {\partial \mathbf {r} _{i}}{\partial q_{j}}}$ and using the kinetic energy equation of motion (blue box above): $Q_{j}={\frac {\mathrm {d} }{\mathrm {d} t}}\left({\frac {\partial T}{\partial {\dot {q}}_{j}}}\right)-{\frac {\partial T}{\partial q_{j}}}=-{\frac {\delta T}{\delta q_{j}}}=\sum _{i=1}^{n}\mathbf {F} _{i}\cdot {\frac {\partial \mathbf {r} _{i}}{\partial q_{j}}},$ For conservative systems (see below) $\mathbf {F} _{i}=-\nabla V_{i}+\mathbf {N} _{i},$ so ${\frac {\delta T}{\delta q_{j}}}=\sum _{i=1}^{n}\mathbf {F} _{i}\cdot {\frac {\partial \mathbf {r} _{i}}{\partial q_{j}}}=\sum _{i=1}^{n}(-\nabla V_{i}+\mathbf {N} _{i})\cdot {\frac {\partial \mathbf {r} _{i}}{\partial q_{j}}}=-\sum _{i=1}^{n}\nabla V_{i}\cdot {\frac {\partial \mathbf {r} _{i}}{\partial q_{j}}}+\sum _{i=1}^{n}\mathbf {N} _{i}\cdot {\frac {\partial \mathbf {r} _{i}}{\partial q_{j}}}=-{\frac {\partial V}{\partial q_{j}}}+N_{j}$ and ${\frac {\delta T}{\delta q_{j}}}={\frac {\mathrm {d} }{\mathrm {d} t}}\left({\frac {\partial (L+V)}{\partial {\dot {q}}_{j}}}\right)-{\frac {\partial (L+V)}{\partial q_{j}}}=-{\frac {\delta L}{\delta {\dot {q}}_{j}}}-{\frac {\partial V}{\partial q_{j}}}$ equating leads to $N_{j}=-{\frac {\delta L}{\delta {\dot {q}}_{j}}}$ and finally equating to Lagrange's equations of the first kind implies: $N_{j}=\sum _{i=1}^{e}\lambda _{i}{\frac {\partial F_{i}}{\partial r_{j}}}$ So each constraint equation corresponds to a constraint force (in a conservative system).

Lagrange equations of the second kind

If the Lagrangian of a system is known, then the equations of motion of the system may be obtained by a direct substitution of the expression for the Lagrangian into the Euler–Lagrange equation. The Lagrangian of a given system is not unique, and two Lagrangians describing the same system can differ by the total derivative (not partial) with respect to time of some function f(q, t)</math>, that is

$L'=L+{\frac {\mathrm {d} f(q,t)}{\mathrm {d} t}}$

However, solving any equivalent Lagrangians will give the same equations of motion.

The Lagrangian in many classical systems is a function of generalized coordinates q_i and their velocities dq_i/dt. These coordinates and velocities are, in their turn, parametric functions of time t:

$L(q_{1}(t),q_{2}(t),\ldots ,\dots {q}_{1}(t),\dots {q}_{2}(t),\ldots ,t)$

In the classical view, time is an independent variable and q_i (and dq_i/dt) are dependent variables as is often seen in phase space explanations of systems.

Euler–Lagrange equations

For any system with m degrees of freedom, the Lagrange equations include m generalized coordinates and m generalized velocities. Below, we sketch out the derivation of the Lagrange equations of the second kind. In this context, V is used rather than U for potential energy and T replaces K for kinetic energy. See the references for more detailed and more general derivations.

The equations of motion in Lagrangian mechanics are the Lagrange equations of the second kind, also known as the Euler–Lagrange equations:

Lagrange's equations (2nd kind)

${\frac {\mathrm {d} }{\mathrm {d} t}}\left({\frac {\partial L}{\partial {\dot {q}}_{j}}}\right)={\frac {\partial L}{\partial q_{j}}}$

where j = 1, 2,...m represents the jth degree of freedom, q_j are the generalized coordinates, and ${\dot {q}}_{j}$ are the generalized velocities.

Although the mathematics required for Lagrange's equations appears significantly more complicated than Newton's laws, this does point to deeper insights into classical mechanics than Newton's laws alone: in particular, symmetry and conservation. In practice it's often easier to solve a problem using the Lagrange equations than Newton's laws, because the minimum generalized coordinates q_i can be chosen by convenience to exploit symmetries in the system, and constraint forces are incorporated into the geometry of the problem. There is one Lagrange equation for each generalized coordinate q_i.

For a system of many particles, each particle can have different numbers of degrees of freedom from the others. In each of the Lagrange equations, T is the total kinetic energy of the system, and V the total potential energy.

Dissipation function

Main article: Rayleigh dissipation function

In a more general formulation, the forces could be both conservative and viscous. If an appropriate transformation can be found from the F_i, Rayleigh suggests using a dissipation function, D, of the following form:

$D={\frac {1}{2}}\sum _{j=1}^{m}\sum _{k=1}^{m}C_{jk}{\dot {q}}_{j}{\dot {q}}_{k}.$

where C_jk are constants that are related to the damping coefficients in the physical system, though not necessarily equal to them

If D is defined this way, then

$Q_{j}=-{\frac {\partial V}{\partial q_{j}}}-{\frac {\partial D}{\partial {\dot {q}}_{j}}}$

and

$0={\frac {\mathrm {d} }{\mathrm {d} t}}\left({\frac {\partial L}{\partial {\dot {q}}_{j}}}\right)-{\frac {\partial L}{\partial q_{j}}}+{\frac {\partial D}{\partial {\dot {q}}_{j}}}.$

Derivations of Lagrange's equations of the second kind

D-Alembert's principle and action in the Lagrangian formulation

The importance of the Lagrangian is derived from D'Alembert's principle, which asserts that the virtual work of any reversible variations subject to the constraints of the system is zero:

$\sum _{i}(\mathbf {F} _{i}-m_{i}\mathbf {a} _{i})\cdot \delta \mathbf {r} _{i}=0$

The integration of this principle over time for a conservative force is

${\begin{aligned}\int _{t_{1}}^{t_{2}}\sum _{i}(\mathbf {F} _{i}-m_{i}\mathbf {a} _{i})\cdot \delta \mathbf {r} _{i}\,dt&=\int _{t_{1}}^{t_{2}}\delta \left(-V+{\frac {1}{2}}\sum _{i}m_{i}v_{i}^{2}\right)\,dt-\left[\sum _{i}m_{i}\mathbf {v} _{i}\cdot \delta \mathbf {r} _{i}\right]_{t_{1}}^{t_{2}}\\&=\delta \int _{t_{1}}^{t_{2}}L\,dt-\left[\sum _{i}m_{i}\mathbf {v} _{i}\cdot \delta \mathbf {r} _{i}\right]_{t_{1}}^{t_{2}}\end{aligned}}$

If the endpoints are fixed, then the last term vanishes, and we have arrived at Hamilton's principle:

$\delta \int _{t_{1}}^{t_{2}}L\,dt=0.$

Hamilton's principle

The Euler–Lagrange equations follow directly from Hamilton's principle, and are mathematically equivalent. From the calculus of variations, any functional of the form:

$J=\int _{x_{1}}^{x_{2}}F(x,y,y')\mathrm {d} x$

leads to the general Euler–Lagrange equation for stationary value of J. (see main article for derivation):

${\frac {\mathrm {d} }{\mathrm {d} x}}{\frac {\partial F}{\partial y'}}={\frac {\partial F}{\partial y}}$

Then making the replacements:

$x\rightarrow t,\quad y\rightarrow q,\quad y'\rightarrow {\dot {q}},\quad F\rightarrow L,\quad J\rightarrow {\mathcal {S}}$

yields the Lagrange equations for mechanics. Since mathematically Hamilton's equations can be derived from Lagrange's equations (by a Legendre transformation) and Lagrange's equations can be derived from Newton's laws, all of which are equivalent and summarize classical mechanics, this means classical mechanics is fundamentally ruled by a variation principle (Hamilton's principle above).

Generalized forces

For a conservative system, since the potential field is only a function of position, not velocity, Lagrange's equations also follow directly from the equation of motion above:

$Q_{j}={\frac {\mathrm {d} }{\mathrm {d} t}}\left({\frac {\partial {\mathcal {(}}L+V)}{\partial {\dot {q}}_{j}}}\right)-{\frac {\partial {\mathcal {(}}L+V)}{\partial q_{j}}}=\left[{\frac {\mathrm {d} }{\mathrm {d} t}}\left({\frac {\partial L}{\partial {\dot {q}}_{j}}}\right)+0\right]-\left[{\frac {\partial L}{\partial q_{j}}}+{\frac {\partial V}{\partial q_{j}}}\right]={\frac {\mathrm {d} }{\mathrm {d} t}}\left({\frac {\partial L}{\partial {\dot {q}}_{j}}}\right)-{\frac {\partial L}{\partial q_{j}}}+Q_{j}.$

simplifying to

${\frac {\mathrm {d} }{\mathrm {d} t}}\left({\frac {\partial L}{\partial {\dot {q}}_{j}}}\right)={\frac {\partial L}{\partial q_{j}}}$

This is consistent with the results derived above and may be seen by differentiating the right side of the Lagrangian with respect to ${\dot {q}}_{j}$ and time, and solely with respect to q_j, adding the results and associating terms with the equations for F_i and Q_j.

Newton's laws

As the following derivation shows, no new physics is introduced, so the Lagrange equations can describe the dynamics of a classical system equivalently as Newton's laws, but not equivalency with Newton's 2nd law by itself which would allow for nonconservative forces such as friction.

Derivation of Lagrange's equations from Newton's 2nd law and D'Alembert's principle

Force and work done (on the particle) Consider a single particle with mass m and position vector r, moving under an applied conservative force F, which can be expressed as the gradient of a scalar potential energy function V(r, t): ${\mathbf {F}}=-{\mathbf {\nabla }}V.\,$ Such a force is independent of third- or higher-order derivatives of r. Consider an arbitrary displacement δr of the particle. The work done by the applied force F is $\delta W={\mathbf {F}}\cdot \delta {\mathbf {r}}.$ Using Newton's second law: ${\mathbf {F}}\cdot \delta {\mathbf {r}}=m{\ddot {\mathbf {r}}}\cdot \delta {\mathbf {r}}.$ Since work is a physical scalar quantity, we should be able to rewrite this equation in terms of the generalized coordinates and velocities. On the left hand side, ${\mathbf {F}}\cdot {\mathbf {\delta }}{\mathbf {r}}=-{\mathbf {\nabla }}V\cdot \displaystyle \sum _{i}{\partial {\mathbf {r}} \over \partial q_{i}}\delta q_{i}=-\displaystyle \sum _{i,j}{\partial V \over \partial r_{j}}{\partial r_{j} \over \partial q_{i}}\delta q_{i}=-\displaystyle \sum _{i}{\partial V \over \partial q_{i}}\delta q_{i}.$ On the right hand side, carrying out a change of coordinates to generalized coordinates, we obtain: $m{\ddot {\mathbf {r}}}\cdot \delta {\mathbf {r}}=m\sum _{j}\left[\sum _{i}{\ddot {r_{i}}}{\partial r_{i} \over \partial q_{j}}\right]\delta q_{j}$ Now integrating by parts the summand with respect to t, then differentiating with respect to t: ${\frac {\mathrm {d} }{\mathrm {d} t}}\int {\ddot {r_{i}}}{\partial r_{i} \over \partial q_{j}}\mathrm {d} t={\frac {\mathrm {d} }{\mathrm {d} t}}\left({\partial r_{i} \over \partial q_{j}}{\dot {r}}_{i}\right)-{\frac {\mathrm {d} }{\mathrm {d} t}}\int {\frac {\mathrm {d} }{\mathrm {d} t}}\left({\partial r_{i} \over \partial q_{j}}\right){\dot {r}}_{i}\mathrm {d} t={\frac {\mathrm {d} }{\mathrm {d} t}}\left({\dot {r}}_{i}{\partial r_{i} \over \partial q_{j}}\right)-{\dot {r}}_{i}{\frac {\mathrm {d} }{\mathrm {d} t}}\left({\partial r_{i} \over \partial q_{j}}\right)$ allows the sum to be written as: $m{\ddot {\mathbf {r}}}\cdot \delta {\mathbf {r}}=m\sum _{j}\left[\sum _{i}\left[{\mathrm {d} \over \mathrm {d} t}\left({\dot {r_{i}}}{\partial r_{i} \over \partial q_{j}}\right)-{\dot {r_{i}}}{\mathrm {d} \over \mathrm {d} t}\left({\partial r_{i} \over \partial q_{j}}\right)\right]\right]\delta q_{j}$ Recognizing that ${\mathrm {d} \over \mathrm {d} t}{\partial r_{j} \over \partial q_{i}}={\partial {\dot {r_{j}}} \over \partial q_{i}},\quad {\partial r_{j} \over \partial q_{i}}={\partial {\dot {r_{j}}} \over \partial {\dot {q_{i}}}},$ we obtain: $m{\ddot {\mathbf {r}}}\cdot \delta {\mathbf {r}}=m\sum _{j}\left[\sum _{i}\left[{\mathrm {d} \over \mathrm {d} t}\left({\dot {r_{i}}}{\partial {\dot {r_{i}}} \over \partial {\dot {q_{j}}}}\right)-{\dot {r_{i}}}{\partial {\dot {r_{i}}} \over \partial q_{j}}\right]\right]\delta q_{j}$ Kinetic and potential energy Now, by changing the order of differentiation, we obtain: $m{\ddot {\mathbf {r}}}\cdot \delta {\mathbf {r}}=m\sum _{j}\left[\sum _{i}\left[{\mathrm {d} \over \mathrm {d} t}{\partial \over \partial {\dot {q_{j}}}}\left({\frac {1}{2}}{\dot {r_{i}}}^{2}\right)-{\partial \over \partial q_{j}}\left({\frac {1}{2}}{\dot {r_{i}}}^{2}\right)\right]\right]\delta q_{j}$ Finally, we change the order of summation: $m{\ddot {\mathbf {r}}}\cdot \delta {\mathbf {r}}=\sum _{j}\left[{\mathrm {d} \over \mathrm {d} t}{\partial \over \partial {\dot {q_{j}}}}\left(\sum _{i}{\frac {1}{2}}m{\dot {r_{i}}}^{2}\right)-{\partial \over \partial q_{j}}\left(\sum _{i}{\frac {1}{2}}m{\dot {r_{i}}}^{2}\right)\right]\delta q_{j}$ Which is equivalent to: $m{\ddot {\mathbf {r}}}\cdot \delta {\mathbf {r}}=\sum _{i}\left[{\mathrm {d} \over \mathrm {d} t}{\partial T \over \partial {\dot {q_{i}}}}-{\partial T \over \partial q_{i}}\right]\delta q_{i}$ where T is total kinetic energy of the system. Applying D'Alembert's principle The equation for the work done becomes $m\mathbf {\ddot {r}} \cdot \delta \mathbf {r} -\mathbf {F} \cdot \delta \mathbf {r} =\sum _{i}\left[{\mathrm {d} \over \mathrm {d} t}{\partial {T} \over \partial {\dot {q_{i}}}}-{\partial {(T-V)} \over \partial q_{i}}\right]\delta q_{i}=0.$ However, this must be true for any set of generalized displacements δqi, so we must have $\left[{\mathrm {d} \over \mathrm {d} t}{\partial {T} \over \partial {\dot {q_{i}}}}-{\partial {(T-V)} \over \partial q_{i}}\right]=0$ for each generalized coordinate δqi. We can further simplify this by noting that V is a function solely of r and t, and r is a function of the generalized coordinates and t. Therefore, V is independent of the generalized velocities: ${\mathrm {d} \over \mathrm {d} t}{\partial {V} \over \partial {\dot {q_{i}}}}=0.$ Inserting this into the preceding equation and substituting L = T − V, called the Lagrangian, we obtain Lagrange's equations: ${\partial {L} \over \partial q_{i}}={\mathrm {d} \over \mathrm {d} t}{\partial {L} \over \partial {\dot {q_{i}}}}.$

When q_i = r_i (i.e. the generalized coordinates are simply the Cartesian coordinates), it is straightforward to check that Lagrange's equations reduce to Newton's second law.

Advantages of the Lagrangian formulation

Importance

The Lagrangian formulation of mechanics is important not just for its broad applications, but also for its role in advancing deep understanding of physics. Although Lagrange only sought to describe classical mechanics, the action principle that is used to derive the Lagrange equation was later recognized to be applicable to quantum mechanics as well.

Physical action and quantum-mechanical phase are related via Planck's constant, and the principle of stationary action can be understood in terms of constructive interference of wave functions.

The same principle, and the Lagrangian formalism, are tied closely to Noether's theorem, which connects physical conserved quantities to continuous symmetries of a physical system.

Lagrangian mechanics and Noether's theorem together yield a natural formalism for first quantization by including commutators between certain terms of the Lagrangian equations of motion for a physical system.

Advantages over other methods

• The formulation is not tied to any one coordinate system – rather, any convenient variables may be used to describe the system; these variables are called "generalized coordinates" q_i and may be any quantitative attributes of the system (for example, strength of the magnetic field at a particular location; angle of a pulley; position of a particle in space; or degree of excitation of a particular eigenmode in a complex system) which are functions of the independent variable(s). This trait makes it easy to incorporate constraints into a theory by defining coordinates that only describe states of the system that satisfy the constraints.

• If the Lagrangian is invariant under a symmetry, then the resulting equations of motion are also invariant under that symmetry. This characteristic is very helpful in showing that theories are consistent with either special relativity or general relativity.

Cyclic coordinates and conservation laws

An important property of the Lagrangian is that conservation laws can easily be read off from it. For example, if the Lagrangian $\scriptstyle L$ does not depend on $\scriptstyle q_{i}$ itself ($\scriptstyle q_{i}$ representing a set of generalized coordinates), then the generalized momentum ($\scriptstyle p_{i}$), given by:

$p_{i}={\frac {\partial L}{\partial {\dot {q}}_{i}}},$

is a conserved quantity, because of Lagrange's equations:

${\dot {p}}_{i}={\frac {d}{dt}}{\frac {\partial L}{\partial {\dot {q}}_{i}}}={\frac {\partial L}{\partial q_{i}}}=0.$

It doesn't matter if $\scriptstyle L$ depends on the time derivative $\scriptstyle {\dot {q}}_{i}$ of that generalized coordinate, since the Lagrangian independence of the coordinate always makes the above partial derivative zero. This is a special case of Noether's theorem. Such coordinates are called "cyclic" or "ignorable".

For example, the conservation of the generalized momentum,

$p_{2}={\frac {\partial L}{\partial {\dot {q}}_{2}}},$

say, can be directly seen if the Lagrangian of the system is of the form

$L(q_{1},q_{3},q_{4},\dots ;{\dot {q}}_{1},{\dot {q}}_{2},{\dot {q}}_{3},{\dot {q}}_{4},\dots ;t)\,.$

Also, if the time t, does not appear in L, then the Hamiltonian, which is related to the Lagrangian by a Legendre transformation, is conserved. This is the energy conservation unless the potential energy depends on velocity, as in electrodynamics.

Examples

The following examples apply Lagrange's equations of the second kind to mechanical problems.

Falling mass

Consider a point mass m falling freely from rest. By gravity a force F = mg is exerted on the mass (assuming g constant during the motion). Filling in the force in Newton's law, we find ${\ddot {x}}=g$ from which the solution

$x(t)={\frac {1}{2}}gt^{2}$

follows (by taking the antiderivative of the antiderivative, and choosing the origin as the starting point). This result can also be derived through the Lagrangian formalism. Take x to be the coordinate, which is 0 at the starting point. The kinetic energy is T = 1⁄2mv² and the potential energy is V = −mgx; hence,

$L=T-V={\frac {1}{2}}m{\dot {x}}^{2}+mgx.$

Then

${\frac {\partial L}{\partial x}}-{\frac {\mathrm {d} }{\mathrm {d} t}}{\frac {\partial L}{\partial {\dot {x}}}}=0=mg-m{\frac {\mathrm {d} {\dot {x}}}{\mathrm {d} t}}$

which can be rewritten as ${\ddot {x}}=g$, yielding the same result as earlier.

Harmonic oscillator

A simple harmonic oscillator; a mass m attached to a spring obeying Hooke's law with spring constant k.

Consider a spring fixed at one end but free to oscillate on the other in one dimension, with a mass m attached to the free end, neglecting gravity or any damping forces, and the spring obeys Hooke's law with spring constant k, Let x be the coordinate, a point along the direction of oscillation, chosen to be zero at the equilibrium point, and the mass can oscillate either side. The kinetic and potential energies are

$T={\frac {1}{2}}m{\dot {x}}^{2}\,,\quad V={\frac {1}{2}}kx^{2}\,,$

hence the Lagrangian is

$L=T-V={\frac {1}{2}}m{\dot {x}}^{2}-{\frac {1}{2}}kx^{2}$

and the equation of motion is that of simple harmonic motion,

${\frac {d}{dt}}{\frac {\partial L}{\partial {\dot {x}}}}={\frac {\partial L}{\partial x}}\quad \Rightarrow \quad m{\ddot {x}}=-kx\,,$

or

${\ddot {x}}=-\omega ^{2}x\,,\quad \omega ={\sqrt {k/m}}\,,$

where ω is the angular frequency of the oscillation. The solutions are sinusoidal oscillations:

$x(t)=A\sin(\omega t)+B\cos(\omega t)$

with A and B are arbitrary constants to be determined from the initial conditions (which have not been specified above). For a harmonic oscillator in higher dimensions, oscillating along a straight line, one can just choose the coordinate along the direction of oscillation and the solution is exactly the same as shown.

There are many complicated and interesting variants of this simple system, which can be solved efficiently using Lagrange's method as shown (although the many degrees of freedom which arise prompt use of the mass matrix). There could be one or many coupled simple harmonic oscillators, with or without damping, with or without some driving force, and in higher dimensions. For example, coupled springs in a mechanical system, the vibrational modes of a molecule, or vibrations of atoms in a crystal. See normal mode for more on this topic.

Pendulum on a movable support

Consider a pendulum of mass m and length ℓ, which is attached to a support with mass M, which can move along a line in the x-direction. Let x be the coordinate along the line of the support, and let us denote the position of the pendulum by the angle θ from the vertical.

Sketch of the situation with definition of the coordinates (click to enlarge)

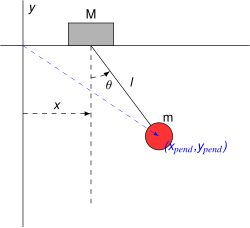
The kinetic energy can then be shown to be

${\begin{array}{rcl}T&=&{\frac {1}{2}}M{\dot {x}}^{2}+{\frac {1}{2}}m\left({\dot {x}}_{\mathrm {pend} }^{2}+{\dot {y}}_{\mathrm {pend} }^{2}\right)\\&=&{\frac {1}{2}}M{\dot {x}}^{2}+{\frac {1}{2}}m\left[\left({\dot {x}}+\ell {\dot {\theta }}\cos \theta \right)^{2}+\left(\ell {\dot {\theta }}\sin \theta \right)^{2}\right],\end{array}}$

and the potential energy of the system is

$V=mgy_{\mathrm {pend} }=-mg\ell \cos \theta .$

The Lagrangian is therefore

${\begin{array}{rcl}L&=&T-V\\&=&{\frac {1}{2}}M{\dot {x}}^{2}+{\frac {1}{2}}m\left[\left({\dot {x}}+\ell {\dot {\theta }}\cos \theta \right)^{2}+\left(\ell {\dot {\theta }}\sin \theta \right)^{2}\right]+mg\ell \cos \theta \\&=&{\frac {1}{2}}\left(M+m\right){\dot {x}}^{2}+m{\dot {x}}\ell {\dot {\theta }}\cos \theta +{\frac {1}{2}}m\ell ^{2}{\dot {\theta }}^{2}+mg\ell \cos \theta \end{array}}$

Now carrying out the differentiations gives for the support coordinate x

${\frac {\mathrm {d} }{\mathrm {d} t}}\left[(M+m){\dot {x}}+m\ell {\dot {\theta }}\cos \theta \right]=0,$

therefore:

$(M+m){\ddot {x}}+m\ell {\ddot {\theta }}\cos \theta -m\ell {\dot {\theta }}^{2}\sin \theta =0$

indicating the presence of a constant of motion. Performing the same procedure for the variable $\theta$ yields:

${\frac {\mathrm {d} }{\mathrm {d} t}}\left[m({\dot {x}}\ell \cos \theta +\ell ^{2}{\dot {\theta }})\right]+m\ell ({\dot {x}}{\dot {\theta }}+g)\sin \theta =0;$

therefore

${\ddot {\theta }}+{\frac {\ddot {x}}{\ell }}\cos \theta +{\frac {g}{\ell }}\sin \theta =0.\,$

These equations may look quite complicated, but finding them with Newton's laws would have required carefully identifying all forces, which would have been much more laborious and prone to errors. By considering limit cases, the correctness of this system can be verified: For example, ${\ddot {x}}\to 0$ should give the equations of motion for a pendulum that is at rest in some inertial frame, while ${\ddot {\theta }}\to 0$ should give the equations for a pendulum in a constantly accelerating system, etc. Furthermore, it is trivial to obtain the results numerically, given suitable starting conditions and a chosen time step, by stepping through the results iteratively.

Two-body central force problem

The basic problem is that of two bodies in orbit about each other attracted by a central force. The Jacobi coordinates are introduced; namely, the location of the center of mass R and the separation of the bodies r (the relative position). The Lagrangian is then

${\begin{aligned}L&=T-U={\frac {1}{2}}M{\dot {\mathbf {R} }}^{2}+\left({\frac {1}{2}}\mu {\dot {\mathbf {r} }}^{2}-U(r)\right)\\&=L_{\mathrm {cm} }+L_{\mathrm {rel} }\end{aligned}}$

where M is the total mass, μ is the reduced mass, and U the potential of the radial force. The Lagrangian is divided into a center-of-mass term and a relative motion term. The R equation from the Euler–Lagrange system is simply:

$M{\ddot {\mathbf {R} }}=0,\,$

resulting in simple motion of the center of mass in a straight line at constant velocity. The relative motion is expressed in polar coordinates (r, θ):

$L={\frac {1}{2}}\mu \left({\dot {r}}^{2}+r^{2}{\dot {\theta }}^{2}\right)-U(r),$

which does not depend upon θ, therefore an ignorable coordinate. The Lagrange equation for θ is then:

${\frac {\partial L}{\partial {\dot {\theta }}}}=\mu r^{2}{\dot {\theta }}=\mathrm {constant} =\ell ,\,$

where ℓ is the conserved angular momentum. The Lagrange equation for r is:

${\frac {\partial L}{\partial r}}={\frac {\mathrm {d} }{\mathrm {d} t}}{\frac {\partial L}{\partial {\dot {r}}}},\,$

or:

$\mu r{\dot {\theta }}^{2}-{\frac {dU}{dr}}=\mu {\ddot {r}}.\,$

This equation is identical to the radial equation obtained using Newton's laws in a co-rotating reference frame, that is, a frame rotating with the reduced mass so it appears stationary. If the angular velocity is replaced by its value in terms of the angular momentum,

${\dot {\theta }}={\frac {\ell }{\mu r^{2}}},\,$

the radial equation becomes:

$\mu {\ddot {r}}=-{\frac {dU}{dr}}+{\frac {\ell ^{2}}{\mu r^{3}}}.\,$

which is the equation of motion for a one-dimensional problem in which a particle of mass μ is subjected to the inward central force −dU/dr and a second outward force, called in this context the centrifugal force:

$F_{\mathrm {cf} }=\mu r{\dot {\theta }}^{2}={\frac {\ell ^{2}}{\mu r^{3}}}.\,$

Of course, if one remains entirely within the one-dimensional formulation, ℓ enters only as some imposed parameter of the external outward force, and its interpretation as angular momentum depends upon the more general two-dimensional problem from which the one-dimensional problem originated.

If one arrives at this equation using Newtonian mechanics in a co-rotating frame, the interpretation is evident as the centrifugal force in that frame due to the rotation of the frame itself. If one arrives at this equation directly by using the generalized coordinates (r, θ) and simply following the Lagrangian formulation without thinking about frames at all, the interpretation is that the centrifugal force is an outgrowth of using polar coordinates. As Hildebrand says: "Since such quantities are not true physical forces, they are often called inertia forces. Their presence or absence depends, not upon the particular problem at hand, but upon the coordinate system chosen." In particular, if Cartesian coordinates are chosen, the centrifugal force disappears, and the formulation involves only the central force itself, which provides the centripetal force for a curved motion.

This viewpoint, that fictitious forces originate in the choice of coordinates, often is expressed by users of the Lagrangian method. This view arises naturally in the Lagrangian approach, because the frame of reference is (possibly unconsciously) selected by the choice of coordinates. Unfortunately, this usage of "inertial force" conflicts with the Newtonian idea of an inertial force. In the Newtonian view, an inertial force originates in the acceleration of the frame of observation (the fact that it is not an inertial frame of reference), not in the choice of coordinate system. To keep matters clear, it is safest to refer to the Lagrangian inertial forces as generalized inertial forces, to distinguish them from the Newtonian vector inertial forces. That is, one should avoid following Hildebrand when he says (p. 155) "we deal always with generalized forces, velocities accelerations, and momenta. For brevity, the adjective "generalized" will be omitted frequently."

It is known that the Lagrangian of a system is not unique. Within the Lagrangian formalism the Newtonian fictitious forces can be identified by the existence of alternative Lagrangians in which the fictitious forces disappear, sometimes found by exploiting the symmetry of the system.

Examples in specific coordinate systems

In Cartesian coordinates

Suppose we have a three-dimensional space in which a particle of mass m moves under the influence of a conservative force $\mathbf {F}$. Since the force is conservative, it corresponds to a potential energy function $V(\mathbf {x} )$ given by $\mathbf {F} =-\nabla V(\mathbf {x} )$. The Lagrangian of the particle can be written

$L(\mathbf {x} ,{\dot {\mathbf {x} }})={\frac {1}{2}}m{\dot {\mathbf {x} }}^{2}-V(\mathbf {x} ).$

The equations of motion for the particle are found by applying the Euler–Lagrange equation

${\frac {\mathrm {d} }{\mathrm {d} t}}\left({\frac {\partial L}{\partial {\dot {x}}_{i}}}\right)-{\frac {\partial L}{\partial x_{i}}}=0,$

where i = 1, 2, 3.

Then

${\frac {\partial L}{\partial x_{i}}}=-{\frac {\partial V}{\partial x_{i}}},$

${\frac {\partial L}{\partial {\dot {x}}_{i}}}={\frac {\partial ~}{\partial {\dot {x}}_{i}}}\left({\frac {1}{2}}m{\dot {\mathbf {x} }}^{2}\right)={\frac {1}{2}}m{\frac {\partial ~}{\partial {\dot {x}}_{i}}}\left({\dot {x}}_{i}^{2}\right)=m{\dot {x}}_{i},$

and

${\frac {\mathrm {d} }{\mathrm {d} t}}\left({\frac {\partial L}{\partial {\dot {x}}_{i}}}\right)=m{\ddot {x}}_{i}.$

Thus

$m{\ddot {\mathbf {x} }}+\nabla V=0,$

which is Newton's second law of motion for a particle subject to a conservative force. Here the time derivative is written conventionally as a dot above the quantity being differentiated, and ∇ is the del operator.

In spherical coordinates

Suppose we have a three-dimensional space using spherical coordinates (r, θ, φ) with the Lagrangian

$L={\frac {m}{2}}({\dot {r}}^{2}+r^{2}{\dot {\theta }}^{2}+r^{2}\sin ^{2}\theta \,{\dot {\varphi }}^{2})-V(r).$

Then the Euler–Lagrange equations are:

$m{\ddot {r}}-mr({\dot {\theta }}^{2}+\sin ^{2}\theta \,{\dot {\varphi }}^{2})+V'=0,$

${\frac {\mathrm {d} }{\mathrm {d} t}}(mr^{2}{\dot {\theta }})-mr^{2}\sin \theta \cos \theta \,{\dot {\varphi }}^{2}=0,$

${\frac {\mathrm {d} }{\mathrm {d} t}}(mr^{2}\sin ^{2}\theta \,{\dot {\varphi }})=0.$

Here the set of parameters s_i is just the time t, and the dynamical variables ϕ_i(s) are the trajectories $\scriptstyle {\vec {x}}(t)$ of the particle.

Despite the use of standard variables such as x, the Lagrangian allows the use of any coordinates, which do not need to be orthogonal. These are "generalized coordinates".

Test particles in fields

A test particle is a particle whose mass and charge are assumed to be so small that its effect on external system is insignificant. It is often a hypothetical simplified point particle with no properties other than mass and charge. Real particles like electrons and up quarks are more complex and have additional terms in their Lagrangians.

Classical test particle with Newtonian gravity

Suppose we are given a particle with mass m kilograms, and position $\mathbf {x}$ meters in a Newtonian gravitation field with potential Φ in J·kg⁻¹. The particle's world line is parameterized by time t seconds. The particle's kinetic energy is:

$T(t)={\tfrac {1}{2}}m\left|{\dot {\mathbf {x} }}(t)\right|^{2}$

and the particle's gravitational potential energy is:

$V(t)=m\Phi (\mathbf {x} (t),t).$

Then its Lagrangian is L joules, where

$L(t)=T(t)-V(t)={\tfrac {1}{2}}m\left|{\dot {\mathbf {x} }}(t)\right|^{2}-m\Phi (\mathbf {x} (t),t).$

Varying $\mathbf {x}$ in the integral (equivalent to the Euler–Lagrange differential equation), we get

$0=\delta \int {L(t)\,\mathrm {d} t}=\int {\delta L(t)\,\mathrm {d} t}$

$=\int {(m{\dot {\mathbf {x} }}(t)\cdot {\dot {\delta \mathbf {x} }}(t)-m\nabla \Phi (\mathbf {x} (t),t)\cdot \delta \mathbf {x} (t))\,\mathrm {d} t}.$

Integrate the first term by parts and discard the total integral. Then divide out the variation to get

$0=-m{\ddot {\mathbf {x} }}(t)-m\nabla \Phi (\mathbf {x} (t),t)$

and thus

$m{\ddot {\mathbf {x} }}(t)=-m\nabla \Phi (\mathbf {x} (t),t)$

(1)

is the equation of motion – two different expressions for the force.

Special relativistic test particle with electromagnetism

In special relativity, the energy (rest energy plus kinetic energy) of a free test particle is

$mc^{2}{\frac {dt}{d\tau }}={\frac {mc^{2}}{\sqrt {1-{\frac {v^{2}(t)}{c^{2}}}}}}=+mc^{2}+{1 \over 2}mv^{2}(t)+{3 \over 8}m{\frac {v^{4}(t)}{c^{2}}}+\dots \,.$

However, the term in the Lagrangian that gives rise to the derivative of the momentum is no longer the kinetic energy.

One possible Lagrangian

$-mc^{2}{\frac {d\tau (t)}{dt}}=-mc^{2}{\sqrt {1-{\frac {v^{2}(t)}{c^{2}}}}}=-mc^{2}+{1 \over 2}mv^{2}(t)+{1 \over 8}m{\frac {v^{4}(t)}{c^{2}}}+\dots$

where c is the vacuum speed of light in m·s⁻¹, τ is the proper time in seconds (i.e. time measured by a clock moving with the particle) and $\scriptstyle v^{2}(t)={\dot {\mathbf {x} }}(t)\cdot {\dot {\mathbf {x} }}(t).$ The second term in the series is just the classical kinetic energy. Suppose the particle has electrical charge q coulombs and is in an electromagnetic field with scalar potential ϕ volts (a volt is a joule per coulomb) and vector potential $\scriptstyle \mathbf {A}$ V·s·m⁻¹. The Lagrangian of a special relativistic test particle in an electromagnetic field is:

$L(t)=-mc^{2}{\sqrt {1-{\frac {v^{2}(t)}{c^{2}}}}}-q\phi (\mathbf {x} (t),t)+q{\dot {\mathbf {x} }}(t)\cdot \mathbf {A} (\mathbf {x} (t),t).$

Varying this with respect to $\mathbf {x}$, we get

$0=-{\frac {d}{dt}}\left({\frac {m{\dot {\mathbf {x} }}(t)}{\sqrt {1-{\frac {v^{2}(t)}{c^{2}}}}}}\right)-q\nabla \phi (\mathbf {x} (t),t)-q{\frac {\partial \mathbf {A} (\mathbf {x} (t),t)}{\partial t}}-q{\dot {\mathbf {x} }}(t)\cdot \nabla \mathbf {A} (\mathbf {x} (t),t)+q\nabla {\mathbf {A} }(\mathbf {x} (t),t)\cdot {\dot {\mathbf {x} }}(t)$

which is

${\frac {d}{dt}}\left({\frac {m{\dot {\mathbf {x} }}(t)}{\sqrt {1-{\frac {v^{2}(t)}{c^{2}}}}}}\right)=q\mathbf {E} (\mathbf {x} (t),t)+q{\dot {\mathbf {x} }}(t)\times \mathbf {B} (\mathbf {x} (t),t)$

which is the equation for the Lorentz force, where:

$\mathbf {E} (\mathbf {x} ,t)=-\nabla \phi (\mathbf {x} ,t)-{\frac {\partial \mathbf {A} (\mathbf {x} ,t)}{\partial t}}$

$\mathbf {B} (\mathbf {x} ,t)=\nabla \times \mathbf {A} (\mathbf {x} ,t)$

are the fields and potentials.

An alternative Lagrangian for a special relativistic test particle is

$L(\tau )={\frac {1}{2}}mu^{\mu }(\tau )u_{\mu }(\tau )+qu^{\mu }(\tau )A_{\mu }(x)$

where u^μ = dx^μ/dτ is the four-velocity of the test particle.

The Euler-Lagrange equations

${\frac {\partial L}{\partial x^{\nu }}}-{\frac {d}{d\tau }}{\frac {\partial L}{\partial u^{\nu }}}=0$

become

$qu^{\mu }{\frac {\partial A_{\mu }}{\partial x^{\nu }}}={\frac {d}{d\tau }}(mu_{\nu }+qA_{\nu })$

General relativistic test particle

In general relativity, the first term generalizes (includes) both the classical kinetic energy and the interaction with the gravitational field. It becomes:

$-mc^{2}{\frac {d\tau (t)}{dt}}=-mc^{2}{\sqrt {-c^{-2}g_{\mu \nu }(x(t)){\frac {dx^{\mu }(t)}{dt}}{\frac {dx^{\nu }(t)}{dt}}}}.$

The Lagrangian of a general relativistic test particle in an electromagnetic field is:

$L(t)=-mc^{2}{\sqrt {-c^{-2}g_{\mu \nu }(x(t)){\frac {dx^{\mu }(t)}{dt}}{\frac {dx^{\nu }(t)}{dt}}}}+q{\frac {dx^{\mu }(t)}{dt}}A_{\mu }(x(t)).$

If the four spacetime coordinates x^µ are given in arbitrary units (i.e. unitless), then g_µν in m² is the rank 2 symmetric metric tensor which is also the gravitational potential. Also, A_µ in V·s is the electromagnetic 4-vector potential.

More generally, suppose the Lagrangian is that of a single particle plus an interaction term L_I

$L=-mc^{2}{\frac {d\tau }{dt}}+L_{I}\,.$

Varying this with respect to the position of the particle x^α as a function of time t gives

$\delta L=m{\frac {dt}{2d\tau }}\delta \left(g_{\mu \nu }{\frac {dx^{\mu }}{dt}}{\frac {dx^{\nu }}{dt}}\right)+\delta L_{I}\,.$

$\delta L=m{\frac {dt}{2d\tau }}\left(g_{\mu \nu ,\alpha }\delta x^{\alpha }{\frac {dx^{\mu }}{dt}}{\frac {dx^{\nu }}{dt}}+2g_{\alpha \nu }{\frac {d\delta x^{\alpha }}{dt}}{\frac {dx^{\nu }}{dt}}\right)+{\frac {\partial L_{I}}{\partial x^{\alpha }}}\delta x^{\alpha }+{\frac {\partial L_{I}}{\partial {\frac {dx^{\alpha }}{dt}}}}{\frac {d\delta x^{\alpha }}{dt}}\,.$

$\delta L={\frac {1}{2}}mg_{\mu \nu ,\alpha }\delta x^{\alpha }{\frac {dx^{\mu }}{d\tau }}{\frac {dx^{\nu }}{dt}}-{\frac {d}{dt}}\left(mg_{\alpha \nu }{\frac {dx^{\nu }}{d\tau }}\right)\delta x^{\alpha }+{\frac {\partial L_{I}}{\partial x^{\alpha }}}\delta x^{\alpha }-{\frac {d}{dt}}\left({\frac {\partial L_{I}}{\partial {\frac {dx^{\alpha }}{dt}}}}\right)\delta x^{\alpha }+{\frac {d(...)}{dt}}\,.$

This gives the equation of motion

$0={\frac {1}{2}}mg_{\mu \nu ,\alpha }{\frac {dx^{\mu }}{d\tau }}{\frac {dx^{\nu }}{dt}}-{\frac {d}{dt}}\left(mg_{\alpha \nu }{\frac {dx^{\nu }}{d\tau }}\right)+f_{\alpha }$

where

$f_{\alpha }={\frac {\partial L_{I}}{\partial x^{\alpha }}}-{\frac {d}{dt}}\left({\frac {\partial L_{I}}{\partial {\frac {dx^{\alpha }}{dt}}}}\right)$

is the non-gravitational force on the particle. (For m to be independent of time, we must have $f_{\alpha }{\tfrac {dx^{\alpha }}{dt}}=0$.)

Rearranging gets the force equation

${\frac {d}{dt}}\left(m{\frac {dx^{\nu }}{d\tau }}\right)=-m\Gamma _{\mu \sigma }^{\nu }{\frac {dx^{\mu }}{d\tau }}{\frac {dx^{\sigma }}{dt}}+g^{\nu \alpha }f_{\alpha }$

where Γ is the Christoffel symbol which is the gravitational force field.

If we let

$p^{\nu }=m{\frac {dx^{\nu }}{d\tau }}$

be the (kinetic) linear momentum for a particle with mass, then

${\frac {dp^{\nu }}{dt}}=-\Gamma _{\mu \sigma }^{\nu }p^{\mu }{\frac {dx^{\sigma }}{dt}}+g^{\nu \alpha }f_{\alpha }$

and

${\frac {dx^{\nu }}{dt}}={\frac {p^{\nu }}{p^{0}}}$

hold even for a massless particle.

Lagrangian mechanics in other contexts

The Hamiltonian, denoted by H, is obtained by performing a Legendre transformation on the Lagrangian, which introduces new variables, canonically conjugate to the original variables. This doubles the number of variables, but makes differential equations first order. The Hamiltonian is the basis for an alternative formulation of classical mechanics known as Hamiltonian mechanics. It is a particularly ubiquitous quantity in quantum mechanics (see Hamiltonian (quantum mechanics)).

In 1948, Feynman discovered the path integral formulation extending the principle of least action to quantum mechanics for electrons and photons. In this formulation, particles travel every possible path between the initial and final states; the probability of a specific final state is obtained by summing over all possible trajectories leading to it. In the classical regime, the path integral formulation cleanly reproduces Hamilton's principle, and Fermat's principle in optics.

Dissipation (i.e. non-conservative systems) can also be treated with an effective Lagrangian formulated by a certain doubling of the degrees of freedom; see.

Uses in Engineering

Circa 1963 Lagrangians were a general part of the engineering curriculum, but a quarter of a century later, even with the ascendency of dynamical systems, they were dropped as requirements for some engineering programs, and are generally considered to be the domain of theoretical dynamics. Circa 2003 this changed dramatically, and Lagrangians are not only a required part of many ME and EE graduate-level curricula, but also find applications in finance, economics, and biology, mainly as the basis of the formulation of various path integral schemes to facilitate the solution of parabolic partial differential equations via random walks.

Circa 2013, Lagrangians find their way into hundreds of direct engineering solutions, including robotics, turbulent flow analysis (Lagrangian and Eulerian specification of the flow field), signal processing, microscopic component contact and nanotechnology (superlinear convergent augmented Lagrangians), gyroscopic forcing and dissipation, semi-infinite supercomputing (which also involve Lagrange multipliers in the subfield of semi-infinite programming), chemical engineering (specific heat linear Lagrangian interpolation in reaction planning), civil engineering (dynamic analysis of traffic flows), optics engineering and design (Lagrangian and Hamiltonian optics) aerospace (Lagrangian interpolation), force stepping integrators, and even airbag deployment (coupled Eulerian-Lagrangians as well as SELM—the stochastic Eulerian Lagrangian method).

See also

• Canonical coordinates
• Functional derivative
• Generalized coordinates
• Hamiltonian mechanics
• Hamiltonian optics
• Lagrangian analysis (applications of Lagrangian mechanics)
• Lagrangian point
• Lagrangian system‎
• Non-autonomous mechanics
• Restricted three-body problem
• Plateau's problem

Further reading

• Landau, L.D. and Lifshitz, E.M. Mechanics, Pergamon Press.
• Gupta, Kiran Chandra, Classical mechanics of particles and rigid bodies (Wiley, 1988).
• Goldstein, Herbert, Classical Mechanics, Addison Wesley.
• Cassel, Kevin W.: Variational Methods with Applications in Science and Engineering, Cambridge University Press, 2013.

External links

• Tong, David, Classical Dynamics Cambridge lecture notes
• Principle of least action interactive Excellent interactive explanation/webpage
• Joseph Louis de Lagrange - Œuvres complètes (Gallica-Math)