Bounded function: Difference between revisions
m Reverted 1 edit by 2401:4900:16C7:9315:2C1C:CC7E:4B82:9D18 identified as test/vandalism using STiki |
Clean some definitions, added and expanded related notion section |
||
| Line 5: | Line 5: | ||
[[for all]] ''x'' in ''X''. A function that is ''not'' bounded is said to be '''unbounded'''. |
[[for all]] ''x'' in ''X''. A function that is ''not'' bounded is said to be '''unbounded'''. |
||
If ''f'' is real-valued and ''f''(''x'') ≤ ''A'' for all ''x'' in ''X'', then the function is said to be '''bounded (from) above''' by ''A''. If ''f''(''x'') ≥ ''B'' for all ''x'' in ''X'', then the function is said to be '''bounded (from) below''' by ''B''. A real-valued function is bounded if and only if it is bounded from above and below. |
|||
| ⚫ | |||
The concept should not be confused with that of a [[bounded operator]]. |
|||
| ⚫ | |||
''a''<sub>1</sub>, ''a''<sub>2</sub>, ...) is bounded if there exists a real number ''M'' such that |
|||
:<math>|a_n|\le M</math> |
:<math>|a_n|\le M</math> |
||
for every natural number ''n''. The set of all bounded sequences |
for every natural number ''n''. The set of all bounded sequences forms the [[sequence space]] <math>l^\infty</math>. |
||
The definition of boundedness can be '''generalized''' to functions ''f : X → Y'' taking values in a more general space ''Y'' by requiring that the image ''f(X)'' is a [[bounded set]] in ''Y''. |
|||
== Related Notions == |
|||
:<math>d(f(x), a)\le M</math> |
|||
Weaker than boundedness is [[local boundedness]]. A family of bounded functions may be [[Uniform boundedness|uniformly bounded]]. |
|||
A [[bounded operator]] ''T : X → Y'' is not a bounded function in the sense of this page's definition (unless ''T = 0''), but has the weaker property of '''preserving boundedness''': Bounded sets ''M ⊆ X'' are mapped to bounded sets ''T(M) ⊆ Y.'' This definition can be extended to any function ''f'' : ''X'' → ''Y'' if ''X'' and ''Y'' allow for the concept of a bounded set. |
|||
for all ''x'' in ''X''. |
|||
If this is the case, there is also such an ''M'' for each other ''a'', by the triangle inequality. |
|||
==Examples== |
==Examples== |
||
* The function |
* The function sin : '''R''' → '''R''' is bounded. |
||
| ⚫ | * The function <math>f(x)=(x^2-1)^{-1}</math>defined for all real ''x'' except for −1 and 1 is unbounded. As ''x'' approaches −1 or 1, the values of this function get larger and larger in magnitude. This function can be made bounded if one considers its domain to be, for example, [2, ∞) or (−∞, −2]. |
||
* The function |
|||
:: <math>f(x)=\frac{1}{x^2-1}</math> |
|||
| ⚫ | |||
| ⚫ | |||
* The function |
|||
| ⚫ | |||
:: <math>f(x)=\frac{1}{x^2+1}</math> |
|||
*All complex-valued functions ''f'' : '''R''' → '''C''' which are [[Entire function|entire]] are either unbounded or constant as a consequence of [[Liouville's theorem (complex analysis)|Liouville's theorem]]. In particular, the complex sin : '''C''' → '''C''' must be unbounded since it's entire. |
|||
| ⚫ | |||
| ⚫ | |||
** Note that for example <math>f(x) \neq \frac{1}{x}</math>, because <math>\lim_{h\rightarrow 0}f(h) = \infty \notin \mathbb{R}</math> |
|||
* The function ''f'' which takes the value 0 for ''x'' [[rational number]] and 1 for ''x'' [[irrational number]] (cf. [[Nowhere continuous function#Dirichlet function|Dirichlet function]]) ''is'' bounded. Thus, a function does not need to be "nice" in order to be bounded. The set of all bounded functions defined on [0, 1] is much bigger than the set of [[continuous function]]s on that interval. |
* The function ''f'' which takes the value 0 for ''x'' [[rational number]] and 1 for ''x'' [[irrational number]] (cf. [[Nowhere continuous function#Dirichlet function|Dirichlet function]]) ''is'' bounded. Thus, a function does not need to be "nice" in order to be bounded. The set of all bounded functions defined on [0, 1] is much bigger than the set of [[continuous function]]s on that interval. |
||
| Line 37: | Line 32: | ||
* [[Bounded set]] |
* [[Bounded set]] |
||
* [[Support (mathematics)#Compact support|Compact support]] |
* [[Support (mathematics)#Compact support|Compact support]] |
||
*[[Local boundedness]] |
|||
* [[Uniform boundedness]] |
* [[Uniform boundedness]] |
||
Revision as of 13:16, 14 January 2019
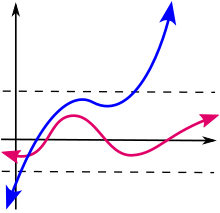
In mathematics, a function f defined on some set X with real or complex values is called bounded, if the set of its values is bounded. In other words, there exists a real number M such that
for all x in X. A function that is not bounded is said to be unbounded.
If f is real-valued and f(x) ≤ A for all x in X, then the function is said to be bounded (from) above by A. If f(x) ≥ B for all x in X, then the function is said to be bounded (from) below by B. A real-valued function is bounded if and only if it is bounded from above and below.
An important special case is a bounded sequence, where X is taken to be the set N of natural numbers. Thus a sequence f = (a0, a1, a2, ...) is bounded if there exists a real number M such that
for every natural number n. The set of all bounded sequences forms the sequence space .
The definition of boundedness can be generalized to functions f : X → Y taking values in a more general space Y by requiring that the image f(X) is a bounded set in Y.
Related Notions
Weaker than boundedness is local boundedness. A family of bounded functions may be uniformly bounded.
A bounded operator T : X → Y is not a bounded function in the sense of this page's definition (unless T = 0), but has the weaker property of preserving boundedness: Bounded sets M ⊆ X are mapped to bounded sets T(M) ⊆ Y. This definition can be extended to any function f : X → Y if X and Y allow for the concept of a bounded set.
Examples
- The function sin : R → R is bounded.
- The function defined for all real x except for −1 and 1 is unbounded. As x approaches −1 or 1, the values of this function get larger and larger in magnitude. This function can be made bounded if one considers its domain to be, for example, [2, ∞) or (−∞, −2].
- The function defined for all real x is bounded.
- Every continuous function f : [0, 1] → R is bounded. More generally, any continuous function from a compact space into a metric space is bounded.
- All complex-valued functions f : R → C which are entire are either unbounded or constant as a consequence of Liouville's theorem. In particular, the complex sin : C → C must be unbounded since it's entire.
- The function f which takes the value 0 for x rational number and 1 for x irrational number (cf. Dirichlet function) is bounded. Thus, a function does not need to be "nice" in order to be bounded. The set of all bounded functions defined on [0, 1] is much bigger than the set of continuous functions on that interval.





