Greatest element and least element

In mathematics, especially in order theory, the greatest element of a subset $S$ of a partially ordered set (poset) is an element of $S$ that is greater than every other element of $S$ . The term least element is defined dually, that is, it is an element of S that is smaller than every other element of $S$ .

Definitions

Let $(P, \leq)$ be a preordered set and let $S \subseteq P$ . An element $g \in P$ is said to be a greatest element of $S$ if $g \in S$ and if it satisfies

s \leq g

for all

s \in S

.

If $S$ has a greatest element and if $(P, \leq)$ is a partially ordered set then it is necessarily unique and so it is called the greatest element of $S$ .

By using $\,\geq \,$ instead of $\,\leq \,$ in the above definition, one defines the least element of $S$ . Explicitly, an element $l \in P$ is said to be a least element of $S$ if $l \in S$ and if it satisfies

l \leq s

for all

s \in S

.

If $(P, \leq)$ has a greatest element (resp. a least element) then this element is also called a top (resp. a bottom) of $(P, \leq)$ .

Relationship to upper/lower bounds

Greatest elements are closely related to upper bounds.

Let $(P, \leq)$ be a preordered set and let $S \subseteq P$ . An upper bound of $S$ in $(P, \leq)$ is an element $u$ such that $u \in P$ and $s \leq u$ for all $s \in S$ .

If $g \in P$ then $g$ is a greatest element of $S$ if and only if $g$ is an upper bound of $S$ in $(P, \leq)$ and $g \in S$ . In particular, any greatest element of $S$ is also an upper bounded of $S$ (in $P$ ) but an upper bound of $S$ in $P$ is a greatest element of $S$ if and only if it belongs to $S$ . In the particular case where $P = S$ , the definition of " $u$ is an upper bound of $S$ in $S$ " becomes: $u$ is an element such that $u \in S$ and $s \leq u$ for all $s \in S$ , which is completely identical to the definition of a greatest element given before. Thus $g$ is a greatest element of $S$ if and only if $g$ is an upper bound of $S$ in $S$ .

If $u$ is an upper bound of $S$ in $P$ that is not an upper bound of $S$ in $S$ (which can happen if and only if $u \notin S$ ) then $u$ can not be a greatest element of $S$ (however, it may be possible that some other element is a greatest element of $S$ ). In particular, it is possible for $S$ to simultaneously not have a greatest element and for there to exist some upper bound of $S$ in $P$ .

Even if a set has some upper bounds, it need not have a greatest element, as shown by the example of the negative real numbers. This example also demonstrates that the existence of a least upper bound (the number 0 in this case) does not imply the existence of a greatest element either.

Contrast to maximal elements and local/absolute maximums

A greatest element of a subset of a preordered set should not be confused with a maximal element of the set, which are elements that are not strictly smaller than any other element in the set. A set can have several maximal elements without having a greatest element. Like upper bounds and maximal elements, greatest elements may fail to exist.

Let $(P, \leq)$ be a partially ordered set and let $S \subseteq P$ . An element $m \in S$ is said to be a maximal element of $S$ if whenever $s \in S$ satisfies $m \leq s$ , then necessarily $s \leq m$ . If $(P, \leq)$ is a partially ordered set then $m \in S$ is a maximal element of $S$ if and only if if there does not exist any $s \in S$ such that $m \leq s$ and $s \neq m$ .

In a totally ordered set the maximal element and the greatest element coincide; and it is also called maximum; in the case of function values it is also called the absolute maximum, to avoid confusion with a local maximum.^[1] The dual terms are minimum and absolute minimum. Together they are called the absolute extrema.

Similar conclusions hold for least elements.

Properties

Throughout, let $(P, \leq)$ be a partially ordered set and let $S \subseteq P$ .

A set $S$ can have at most one greatest element.^{[note 1]} Thus if a set has a greatest element then it is necessarily unique.
If it exists, then the greatest element of $S$ is an upper bound of $S$ that is also contained in $S$ .
If g is the greatest element of S then g is also a maximal element of S^{[note 2]} and moreover, any other maximal element of S will necessarily be equal to g.^{[note 3]}
- Thus if a set $S$ has several maximal elements then it cannot have a greatest element.
If $P$ satisfies the ascending chain condition, a subset $S$ of $P$ has a greatest element if, and only if, it has one maximal element.^{[note 4]}
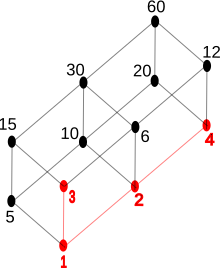
When the restriction of ≤ to S is a total order (S = { 1, 2, 4 } in the topmost picture is an example), then the notions of maximal element and greatest element coincide.^{[note 5]}
- However, this is not a necessary condition for whenever $S$ has a greatest element, the notions coincide, too, as stated above.
If the notions of maximal element and greatest element coincide on every two-element subset $S$ of $P$ , then $\leq$ is a total order on $P$ .^{[note 6]}

Sufficient conditions

A finite chain always has a greatest and a least element.

Top and bottom

The least and greatest element of the whole partially ordered set play a special role and are also called bottom (⊥) and top (⊤), or zero (0) and unit (1), respectively. If both exist, the poset is called a bounded poset. The notation of 0 and 1 is used preferably when the poset is a complemented lattice, and when no confusion is likely, i.e. when one is not talking about partial orders of numbers that already contain elements 0 and 1 different from bottom and top. The existence of least and greatest elements is a special completeness property of a partial order.

Further introductory information is found in the article on order theory.

Examples

The subset of integers has no upper bound in the set $ℝ$ of real numbers.
Let the relation $\leq$ on ${a, b, c, d$ } be given by $a \leq c$ , $a \leq d$ , $b \leq c$ , $b \leq d$ . The set ${a, b$ } has upper bounds $c$ and $d$ , but no least upper bound, and no greatest element (cf. picture).
In the rational numbers, the set of numbers with their square less than 2 has upper bounds but no greatest element and no least upper bound.
In $ℝ$ , the set of numbers less than 1 has a least upper bound, viz. 1, but no greatest element.
In $ℝ$ , the set of numbers less than or equal to 1 has a greatest element, viz. 1, which is also its least upper bound.
In $ℝ²$ with the product order, the set of pairs $(x, y)$ with $0 < x < 1$ has no upper bound.
In $ℝ²$ with the lexicographical order, this set has upper bounds, e.g. $(1, 0)$ . It has no least upper bound.

Notes

^ If $g 1$ and $g 2$ are both greatest, then $g 1 \leq g 2$ and $g 2 \leq g 1$ , and hence $g 1 = g 2$ by antisymmetry.
^ If $g$ is the greatest element of $S$ and $s \in S$ , then $s \leq g$ . By antisymmetry, this renders ( $g \leq s$ and $g \neq s$ ) impossible.
^ If $m'$ is a maximal element, then $m' \leq g$ since $g$ is greatest, hence $m' = g$ since $m'$ is maximal.
^ Only if: see above. — If: Assume for contradiction that $S$ has just one maximal element, $m$ , but no greatest element. Since $m$ is not greatest, some $s 1 \in S$ must exist that is incomparable to $m$ . Hence $s 1 \in S$ cannot be maximal, that is, $s 1 < s 2$ must hold for some $s 2 \in S$ . The latter must be incomparable to $m$ , too, since $m < s 2$ contradicts $m$ 's maximality while $s 2 \leq m$ contradicts the incomparability of $m$ and $s 1$ . Repeating this argument, an infinite ascending chain $s 1 < s 2 < \cdot\cdot\cdot < s n < \cdot\cdot\cdot$ can be found (such that each $s i$ is incomparable to $m$ and not maximal). This contradicts the ascending chain condition.
^ Let $m \in S$ be a maximal element, for any $s \in S$ either $s \leq m$ or $m \leq s$ . In the second case, the definition of maximal element requires that $m = s$ , so it follows that $s \leq m$ . In other words, $m$ is a greatest element.
^ If $a, b \in P$ were incomparable, then $S = {a, b$ } would have two maximal, but no greatest element, contradicting the coincidence.

References

^ The notion of locality requires the function's domain to be at least a topological space.

Davey, B. A.; Priestley, H. A. (2002). Introduction to Lattices and Order (2nd ed.). Cambridge University Press. ISBN 978-0-521-78451-1.

[2] If $g 1$ and $g 2$ are both greatest, then $g 1 \leq g 2$ and $g 2 \leq g 1$ , and hence $g 1 = g 2$ by antisymmetry.

[3] If $g$ is the greatest element of $S$ and $s \in S$ , then $s \leq g$ . By antisymmetry, this renders ( $g \leq s$ and $g \neq s$ ) impossible.

[4] If $m'$ is a maximal element, then $m' \leq g$ since $g$ is greatest, hence $m' = g$ since $m'$ is maximal.

[5] Only if: see above. — If: Assume for contradiction that $S$ has just one maximal element, $m$ , but no greatest element. Since $m$ is not greatest, some $s 1 \in S$ must exist that is incomparable to $m$ . Hence $s 1 \in S$ cannot be maximal, that is, $s 1 < s 2$ must hold for some $s 2 \in S$ . The latter must be incomparable to $m$ , too, since $m < s 2$ contradicts $m$ 's maximality while $s 2 \leq m$ contradicts the incomparability of $m$ and $s 1$ . Repeating this argument, an infinite ascending chain $s 1 < s 2 < \cdot\cdot\cdot < s n < \cdot\cdot\cdot$ can be found (such that each $s i$ is incomparable to $m$ and not maximal). This contradicts the ascending chain condition.

[6] Let $m \in S$ be a maximal element, for any $s \in S$ either $s \leq m$ or $m \leq s$ . In the second case, the definition of maximal element requires that $m = s$ , so it follows that $s \leq m$ . In other words, $m$ is a greatest element.

[7] If $a, b \in P$ were incomparable, then $S = {a, b$ } would have two maximal, but no greatest element, contradicting the coincidence.

[1] The notion of locality requires the function's domain to be at least a topological space.

[1]

[note 1]

[note 2]

[note 3]

[note 4]

[note 5]

[note 6]