リーマン球面

リーマン球面は、複素平面で包んだ球面（ある形式の立体射影による ― 詳細は下記参照）として視覚化できる。

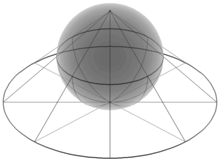
数学においてリーマン球面（リーマンきゅうめん、英語: Riemann sphere）は、無限遠点 ∞ を一点追加して複素平面を拡張したものである。このとき、関係式

1/0 = ∞

を、意味を持ち、整合的であり、かつ有用となるように構成できる。 19 世紀の数学者ベルンハルト・リーマンから名付けられた。 これはまた、以下のようにも呼ばれる。

• 複素射影直線と言い、CP¹ と書く。
• 拡張複素平面と言い、Ĉ または C ∪ {∞} と書く。

純代数的には、無限遠点を追加した複素数全体は、拡張複素数として知られる数体系を構成する。無限遠点を伴う算術は、通常の代数規則すべてには従わず、拡張複素数全体は体を構成しない。しかしリーマン球面は、幾何学的また解析学的に無限遠においてさえもよく振舞い、リーマン面とも呼ばれる 1-次元複素多様体をなす。

複素解析において、リーマン球面は有理型関数の洗練された理論で重要な役割を果たす。 リーマン球面は、射影幾何学や代数幾何学では、複素多様体、射影空間、代数多様体の根源的な事例として常に登場する。 リーマン球面はまた、量子力学その他の物理学の分野等、解析学と幾何学に依存する他の学問分野においても、有用性を発揮している。

拡張複素数

拡張複素数 (extended complex numbers) は複素数 C と ∞ からなる。拡張複素数の集合は C ∪ {∞} と書け、しばしば文字 C に追加の装飾を施して表記される。例えば、Ĉ, C または C_∞。

幾何学的には、拡張複素数の集合はリーマン球面 (Riemann sphere) （あるいは拡張複素平面 (extended complex plane)）と呼ばれる。

演算

複素数の加法は任意の複素数 z に対して

$z+\infty =\infty$

と定義することで拡張され、乗法は任意の 0 でない複素数 z に対して

$z\cdot \infty =\infty$

とし、∞ ⋅ ∞ = ∞ と定義することで拡張される。∞ + ∞, ∞ – ∞, 0 ⋅ ∞ は未定義のままであることに注意すべきである。複素数とは違って、拡張複素数は体をなさない。∞ は乗法逆元をもたないからだ。それでもなお、C ∪ {∞} 上の除法を次のように定義するのが習慣である。0 でないすべての複素数 z に対して

$z/0=\infty \quad {\text{and}}\quad z/\infty =0$

∞/0 = ∞ そして 0/∞ = 0。商 0/0 および ∞/∞ は定義されないままである。

有理関数

任意の有理関数 f(z) = g(z)/h(z) （言い換えるとf(z) は、複素係数の z の、共通因子をもたない2つの多項式関数 g(z) と h(z) の比である）をリーマン球面上の連続関数に拡張できる。具体的には、z₀ を、分母 h(z₀) が 0 だが分子 g(z₀) が 0 でないような複素数とすれば、f(z₀) を ∞ と定義できる。さらに、f(∞) は f(z) の z → ∞ における極限として定義できる。これは有限かもしれないし無限かもしれない。

複素有理関数全体の集合 C(z) は、リーマン球面をリーマン面と見たときに、すべての点で値 ∞ をとる定数関数を除いて、リーマン球面からそれ自身へのあらゆる正則関数をなす。C(z) の関数たちは代数体をなし、球面上の有理関数体 (the field of rational functions on the sphere) として知られている。

例えば、関数

$f(z)={\frac {6z^{2}+1}{2z^{2}-50}}$

が与えられると、z = 5 で分母が 0 なので f(5) = ∞ と定義でき、z → ∞ のとき f(z) → 3 なので f(∞) = 3 と定義できる。これらの定義を用いて、f はリーマン球面からそれ自身への連続関数になる。

複素多様体としてのリーマン球面

リーマン球面は 1-次元複素多様体として、どちらも定義域が複素平面 C に一致する 2 つの局所座標系により記述できる。 ζ と ξ を C 上の複素座標とする。 非零複素数 ζ と非零複素数 ξ を、以下の推移写像（すいいしゃぞう、英: transition function）による等式で関係付ける。

ζ = 1/ξ
ξ = 1/ζ

推移写像は正則であることから、これによりリーマン球面と呼ばれる複素多様体が定義できる。

直感的には、推移写像は、二つの平面をどの様に貼り付けてリーマン球面を作るかを示している。 二つの平面は「表裏反対」に貼り付けられ、各平面の一点（原点）を除き、他の至る部分が互いに重なり合う。 つまり、リーマン球面のほとんど全ての点は、ζ-値と ξ-値の双方を有し、両値は ζ = 1/ξ の関係を有する。 従って、ξ = 0 の点は “1/0” の ζ-値を持つ。 この意味で、ξ-局所座標系の原点は、ζ-局所座標系において “∞” の役割を有する。 対称的に、ζ = 0 の点は 1/0 の ξ-値を持ち、ζ-局所座標系の原点は、ξ-局所座標系に関し ∞ の役割を有する。

位相幾何学的には、結果として得られるリーマン球面は、平面を一点コンパクト化し球面にしたものである。 しかし、リーマン球面は単なる位相的球面ではない。リーマン球面は上手く定義された複素構造を持つ球面であり、球面上の任意の点は、C と正則同相な近傍を有する。 他方、リーマン面の分類論の中心的な結果である一意化定理によれば、単連結な 1 次元複素多様体は、複素平面、双曲平面、リーマン球面の何れかしかない。 勿論、リーマン球面は、閉曲面（境界がないコンパクト曲面）としては唯一のものである。 したがって、2 次元球面には、1 次元複素多様体としての複素構造が一意に存在する。

複素射影直線としてのリーマン球面

リーマン球面は、複素射影直線（ふくそしゃえいちょくせん、英: complex projective line）としても定義することができる。 これは、双方が零ではない複素数の対 (α, β), (α′, β′) に対し、任意の非零複素数 λ によって同値関係

(α, β) ∼ (α′, β′) ⇔ (α′, β′) = (λα, λβ)

を定義し、C² の部分集合であるこの様なすべての対全体の集合に関して商をとった空間である。 座標 ζ を有する複素平面 C は

(α, β) = (ζ, 1)

により複素射影直線の中に写像される。 座標 ξ を有するもう一つの複素平面 C は

(α, β) = (1, ξ)

により複素射影直線の中に写像される。この 2 つの複素局所座標系は、射影直線を被覆する。 非零な ξ, ζ に対し、恒等式

(1, ξ) = (1/ξ, 1) = (ζ, 1)

により、上記のとおり ζ = 1/ξ および ξ = 1/ζ が推移写像であることがわかる。 この様に取り扱うことにより、リーマン球面は射影幾何学に最も容易に関係付けられる。 例えば、複素射影平面における任意の直線（または滑らかな円錐曲線）は、複素射影直線に正則同相である。 これはまた、この記事の後半に登場する球面の自己同型の研究において便利である。

球面としてのリーマン球面

複素数 A をリーマン球面上の一点 α に写す立体射影

リーマン球面は、3 次元実空間 R³ 内の単位球面 S² = { (x, y, z) ∈ R³  |  x² + y² + z² = 1} として視覚化できる。 そのため、点 (0, 0, 1) を除いた単位球面から平面 z = 0 への立体射影を考え、ζ = x + iy により複素平面と同一視する。 直交座標 (x, y, z) と球座標 (φ, θ) （φ は天頂角、θ は方位角） により、立体射影は、以下のとおり書ける。

$\zeta ={\frac {x+iy}{1-z}}=\left(\cot {\frac {\phi }{2}}\right)e^{i\theta }$

同様に、点 (0, 0, −1) から平面 z = 0 への立体射影は、ξ = x − iy によりもう 1 つの複素平面の複写と同一視し、

$\xi ={\frac {x-iy}{1+z}}=\left(\tan {\frac {\phi }{2}}\right)e^{-i\theta }$

と書ける。 （二つの複素平面は、平面 z = 0 と異なる方法で同一視される。 球面上の向きを整合的に保つため、双方の向きを反対にすることが必要であり、特に、複素共軛は推移写像を正則にする。） ζ-座標と ξ-座標の推移写像は、一方の射影と他方の逆数を組み合わせて得られる。 これは、上記のとおり ζ = 1/ξ および ξ = 1/ζ である。 この様にして、単位球面はリーマン球面に可微分同相である。

この可微分同相により、ζ-局所座標系の単位円、ξ-局所座標系の単位円、単位球面の赤道は、すべて同一視される。 単位円盤 | ζ | < 1 は南半球 z < 0 と同一視され、単位円盤 | ξ | < 1 は北半球 z > 0 と同一視される。

計量

リーマン球面には特定のリーマン計量が標準的に備わっている訳ではない。しかしリーマン球面の複素構造は、等角同値を除き一意に計量を決定する（二つの計量は、正値の滑らかな関数を掛けただけしか差がないとき、等角同値という）。 逆に、向きの付いた曲面上の任意の計量は複素構造を一意に決定する。これは等角同値を除き計量に完全に依存して定まる。従って、向きの付いた曲面上の複素構造はその曲面上の計量の等角同値類と一対一に対応する。

ある等角同値類の中で、便利な特性を有する計量を代表元として選ぶために、等角対称性を使うことができる。特に、任意の等角同値類には定曲率の完備な計量が常に存在する。

リーマン球面の場合には、ガウス・ボンネの定理により、定曲率計量は、必ず正の曲率 K を有することが帰結される。 そこでこの計量は、立体射影を通じて R³ 内の半径 $1/{\sqrt {K}}$ の球面の距離を保たなければならない。 リーマン球面の ζ-局所座標系では、K = 1 である計量は、以下により与えられる。

$ds^{2}=\left({\frac {2}{1+|\zeta |^{2}}}\right)^{2}|d\zeta |^{2}={\frac {4}{\left(1+\zeta {\bar {\zeta }}\right)^{2}}}\,d\zeta \,d{\bar {\zeta }}$

実座標 ζ = u + iv において、この式は、以下のとおりとなる。

$ds^{2}={\frac {4}{\left(1+u^{2}+v^{2}\right)^{2}}}\left(du^{2}+dv^{2}\right)$

定数因子を除き、この計量は複素射影空間（リーマン球面はその一例である）のフビニ・スタディー計量に一致する。

逆に、S を（抽象的な微分多様体または位相多様体としての）球面とする。 一意化定理により、S には複素構造が一意に存在する。 S 上の任意の計量は、円形計量（英: round metric）に共形同値である。 これらすべての計量は、同一の共形幾何学を決定する。 従って「円形性」は共形幾何学の不変量でないので、円形計量はリーマン球面にとって内在的なものではない。 リーマン球面は単に共形多様体に過ぎず、リーマン多様体ではない。 しかし、リーマン球面上でリーマン幾何学をする必要があるのであれば、円形計量は自然な選択である。

自己同型

立体射影により球面上および平面上に作用する一次分数変換

あらゆる数学的対象の研究は、自己同型群、つまりその対象から自身への写像であって、同対象の主要な構造を保存するものがなす群を理解することにより促進される。 リーマン球面の場合、自己同型は、リーマン球面から自身への可逆な双正則写像である。 このような写像は、メビウス変換（英: Möbius transformation）とも呼ばれる一次分数変換のみであることが知られている。一次分数変換は

$f(\zeta )={\frac {a\zeta +b}{c\zeta +d}}$

なる形に書かれる関数である。ここに a, b, c, d は ad − bc ≠ 0 を満たす複素数である。一次分数変換には、伸縮と回転 (ζ → aζ)、平行移動 (ζ → ζ + b)、相似・実軸対称 (ζ → 1/ζ等がある。実際のところ、任意の一次分数変換はこれらの合成により記述できる。

一次分数変換は複素射影曲線上の変換と見るとわかり易い。変換 f は射影座標により

$f(\alpha ,\beta )=(a\alpha +b\beta ,c\alpha +d\beta )={\begin{pmatrix}\alpha &\beta \end{pmatrix}}{\begin{pmatrix}a&c\\b&d\end{pmatrix}}$

と書くことができる。 この様に、一次分数変換は、2-次複素正則行列により記述することができる。 ここで、二つの行列は、それらが非零定数倍だけ異なるとき、かつその場合に限り、同一の一次分数変換を表す。したがって、一次分数変換の全体は射影線型変換の全体 PGL₂(C) に完全に一致する。

リーマン球面にフビニ・スタディー計量を入れると、全ての一次分数変換が等長になるとは限らない。 例えば、伸縮と平行移動はそうでない。 等長写像全体は PGL₂(C) の真の部分群 PSU₂ を形成する。この部分群は回転群 SO(3), つまり R³ 内の単位球面の等長変換群と同型である。

応用

複素解析で、複素平面（またはリーマン球面）上の有理型関数とは、正則関数 f と g の比 f/g である。 複素数全体への写像としては、g = 0 である限り、これは定義されない。 しかし、g = 0 であっても、複素射影直線への正則写像 (f, g) は整合的に定義され、これを含む。 この構成法は正則および有理型関数の研究に有用である。 例えば、コンパクトなリーマン球面上には定数でない複素数値正則写像が存在しないが、複素射影直線への正則写像は沢山存在する。

リーマン球面は物理学で多くの応用を有する。 量子力学において、複素射影直線上の点は、光子の偏光状態、スピン 1/2 の有質量粒子のスピン状態、および一般に 2 状態の粒子の自然な値を示す。 リーマン球面は、天球の相対論的モデルに使用することも推奨されてきた。 弦理論 では、弦の世界面はリーマン球面であり、最も単純なリーマン面としてのリーマン球面は重要な役割を演じる。 これは、ツイスター理論においても重要である。

参考文献

• Jones, G. A.; Singerman, D. (1987). Complex Functions: An Algebraic and Geometric Viewpoint. Cambridge University Press. ISBN 0-521-31366-X. Zbl 0608.30001. https://books.google.co.jp/books?id=_U3RXDy7UQcC 

外部リンク

• Möbius Transformations Revealed - YouTube, by Douglas N. Arnold and Jonathan Rogness (a video by two University of Minnesota professors explaining and illustrating Möbius transformations using stereographic projection from a sphere)
• Weisstein, Eric W. "Riemann Sphere". mathworld.wolfram.com (英語).
• Riemann sphere in nLab
• closed complex plane - PlanetMath.（英語）
• Riemann sphere - PlanetMath.（英語）
• Definition:Riemann Sphere at ProofWiki
• Solomentsev, E.D. (2001), “Extended complex plane”, in Hazewinkel, Michiel, Encyclopedia of Mathematics, Springer, ISBN 978-1-55608-010-4, https://www.encyclopediaofmath.org/index.php?title=Extended_complex_plane 
• Solomentsev, E.D. (2001), “Riemann_sphere”, in Hazewinkel, Michiel, Encyclopedia of Mathematics, Springer, ISBN 978-1-55608-010-4, https://www.encyclopediaofmath.org/index.php?title=Riemann_sphere