「クロス積」の版間の差分
→分配律: 角括弧表記のtypo |
|||
| (8人の利用者による、間の30版が非表示) | |||
| 1行目: | 1行目: | ||
[[ファイル:Cross_product_parallelogram.svg|右|サムネイル|3次元ベクトル {{mvar|'''a'''}}, {{mvar|'''b'''}} のクロス積({{math|''a'' × ''b''}})。クロス積は、{{mvar|'''a'''}}, {{mvar|'''b'''}} のなす[[平行四辺形]]の[[面積]]に等しい大きさを持ち、平行四辺形に[[垂直]]なベクトルとなる。]] |
|||
'''ベクトル積'''({{Lang-en|vector product}})とは、[[ベクトル解析]]において、[[3次元]]の[[向き付け]]られた[[内積空間]]において定義される、2つの[[ベクトル空間|ベクトル]]から新たなベクトルを与える[[二項演算]]である。2つのベクトル '''''a''''', '''''b''''' (以下、ベクトルは太字で表記)のベクトル積は '''''a'''''×'''''b''''' や ['''''a''''','''''b'''''] で表される。演算の記号から'''クロス積'''({{en|cross product}})と呼ばれることもある。2つのベクトルから[[スカラー (数学)|スカラー]]を与える[[二項演算]]である[[内積]]に対して'''外積'''(がいせき)とも呼ばれるが、英語で{{en|outer product}}は[[直積 (ベクトル)|直積]]を意味するので注意を要する。ベクトル積を拡張した[[外積代数]]があり、ベクトル積はその3次元における特殊な場合である。 |
|||
{{読み仮名|'''クロス積'''|クロスせき|{{lang-en-short|cross product}}}}は、[[3次元]]空間(3次元[[有向]][[内積空間]])において定義される、2つの[[ベクトル空間|ベクトル]]から新たなベクトルを与える[[二項演算]]である。 |
|||
2つのベクトル {{mvar|a}}, {{mvar|b}} のクロス積は[[×|乗算記号]]を用いて {{math|''a'' × ''b''}}、あるいは[[角括弧]]を用いて {{math|[''a'', ''b'']}} と表される。 |
|||
== 呼称 == |
|||
「クロス積」という呼称は、積の記号に十字([[乗算記号|×]])を用いることに由来する(同様にベクトルの[[内積]]は点([[中黒|⋅]])を用いることから[[ドット積]]と呼ばれる)。またクロス積の別称として、{{読み仮名|'''ベクトル積'''|ベクトルせき|{{lang-en-short|vector product}}}}がある。「ベクトル積」は積 {{math|''a'' × ''b''}} がベクトルとなることに由来する(同様に積 {{math|''a'' ⋅ ''b''}} はスカラーとなるため、ドット積はスカラー積とも呼ばれる)。 |
|||
[[日本語]]や[[中国語]]では、クロス積({{zh-hant|叉積}}、{{zh-hans|叉积}})をしばしば'''外積'''({{zh-hant|外積}}、{{zh-hans|外积}})と呼び、しばしば同義語として扱う。しかし「外積」という語は、より一般には[[外積代数]]における楔積も指し、必ずしも「クロス積」とは一致しない。 |
|||
楔積とクロス積を区別のため、前者を外積と呼び後者をクロス積と呼ぶ。 |
|||
{{en|outer product}} もまた「外積」と訳されるが、こちらは[[直積 (ベクトル)|直積]]({{en|direct product}})を意味する。 |
|||
== 表記 == |
|||
2つのベクトル {{mvar|'''a'''}}, {{mvar|'''b'''}} のクロス積は、以下のように表記される。 |
|||
* [[乗算記号]]を用いる場合:<math>\boldsymbol{a} \times \boldsymbol{b} </math> |
|||
* [[角括弧]]を用いる場合:<math>[\boldsymbol{a}, \boldsymbol{b}] </math> |
|||
== 定義 == |
== 定義 == |
||
[[File:Right hand rule cross product.svg|サムネイル|右|[[右手の法則]]によるクロス積の向き]] |
|||
3次元の向き付けられたベクトル空間におけるベクトル積 [ · , · ] は、任意のベクトル '''''v''''' に対して内積 ( · , · ) との間に |
|||
[[ファイル:Cross_product_vector.svg|右|サムネイル|[[右手系]]の外積]] |
|||
3次元空間上の2つのベクトル {{mvar|'''a'''}}, {{mvar|'''b'''}} のクロス積 {{math|1='''''a''''' × '''''b'''''}} は、以下のように定義される: |
|||
:<math> |
|||
\boldsymbol{a} \times \boldsymbol{b} |
|||
= \left| \boldsymbol{a} \right| |
|||
\left| \boldsymbol{b} \right| |
|||
\sin (\theta) \ \boldsymbol{n} |
|||
</math> |
|||
ただし、{{mvar|θ}} は2つのベクトルのなす角の角度、{{math|{{abs|⋅}}}} は[[ノルム|ベクトルの大きさ]]、{{mvar|'''n'''}} は2つのベクトルがなす平面に対し[[垂直]]な[[単位ベクトル]]を表す({{mvar|'''n'''}} は[[右手系]]になるように取る)。 |
|||
=== 行列式による定義 === |
|||
3次元の向き付けられたベクトル空間におけるクロス積は、任意のベクトル '''''v''''' に対して[[ドット積]]との間に |
|||
{{Indent| |
{{Indent| |
||
<math> |
|||
<math>(\boldsymbol{v}, [\boldsymbol{a}, \boldsymbol{b}]) |
|||
\boldsymbol{v} |
|||
\cdot ( |
|||
\boldsymbol{a} |
|||
\times \boldsymbol{b} |
|||
) |
|||
= \det \langle |
|||
\boldsymbol{v}, |
|||
\boldsymbol{a}, |
|||
\boldsymbol{b} |
|||
\rangle |
|||
</math> |
|||
}} |
}} |
||
の関係を満たすベクトルの二項演算である。ここで 〈 · , · , · 〉 はベクトルを標準的な基底により[[列ベクトル]]と同一視することで得られる3次[[正方行列]]である。det は[[行列式]]を表す。 |
の関係を満たすベクトルの二項演算である。ここで 〈 · , · , · 〉 はベクトルを標準的な基底により[[列ベクトル]]と同一視することで得られる3次[[正方行列]]である。det は[[行列式]]を表す。 |
||
幾何的なベクトルの演算として定義できる。 |
|||
=== 成分による表示 === |
|||
行列式の交代性から、 |
|||
{{Indent|<math>\boldsymbol{a} \cdot (\boldsymbol{a} \times \boldsymbol{b}) |
|||
=\boldsymbol{b} \cdot (\boldsymbol{a} \times \boldsymbol{b} )=0</math>}} |
|||
である。 |
|||
従って、2つのベクトル '''''a'''''、'''''b''''' のクロス積 '''''a'''''×'''''b''''' は、元のベクトル '''''a'''''、'''''b''''' の両方と直交する。言い換えれば、2つのベクトルが作る[[平面]]の[[法線]]と平行な方向を向いている。 |
|||
ただし、法線のどちらの方向に向いているかは座標軸の選び方に依存し、[[右手系]]と[[左手系]]に分けられる。右手系の場合は、'''''a''''' をその始点の周りに180度以下の回転角で回して '''''b''''' に重ねるときに右ねじの進む方向である。すなわち、右手の親指を '''''a'''''、人差し指を'''''b''''' としたときの中指がクロス積 '''''a'''''×'''''b''''' の向きを表す。左手系の場合は、'''''b''''' をその始点の周りに180度以下の回転角で回して '''''a''''' に重ねるときに右ねじの進む向きである。 |
|||
行列式とスカラー積の線型性からクロス積も双線型性をもつ。 特に、2つのベクトル '''''a'''''、'''''b''''' のクロス積 '''''a'''''×'''''b''''' は、元のベクトル '''''a'''''、'''''b''''' の大きさに比例する。 また、二つのベクトル '''''a'''''、'''''b''''' のなす角を ''θ'' とすれば、標準的な基底の下で |
|||
{{Indent|<math>\boldsymbol{a} = |
|||
\begin{pmatrix} |
|||
a \\ 0 \\ 0 \\ |
|||
\end{pmatrix},~ |
|||
\boldsymbol{b} = |
|||
\begin{pmatrix} |
|||
b\cos\theta \\ b\sin\theta \\ 0 \\ |
|||
\end{pmatrix}</math>}} |
|||
と成分表示することができる。これらのクロス積は |
|||
{{Indent|<math>\boldsymbol{a} \times \boldsymbol{b} = |
|||
\begin{pmatrix} |
|||
0 \\ 0 \\ ab\sin\theta \\ |
|||
\end{pmatrix}</math>}} |
|||
となる。従ってクロス積の大きさは |
|||
{{Indent|<math>\vert \boldsymbol{a} \times \boldsymbol{b} \vert |
|||
=\vert \boldsymbol{a} \vert\, \vert \boldsymbol{b} \vert \sin\theta</math>}} |
|||
であり、2つのベクトルが作る[[平行四辺形]]の面積に等しい。 |
|||
== 成分表示 == |
|||
標準的な基底を ('''''e'''{{sub|i}}'','''''e'''{{sub|j}}'')=''δ{{sub|i,j}}'' として、ベクトル '''''a''''' の成分 ''a{{sub|i}}''=('''''e'''{{sub|i}}'','''''a''''') により列ベクトルとの同一視 |
標準的な基底を ('''''e'''{{sub|i}}'','''''e'''{{sub|j}}'')=''δ{{sub|i,j}}'' として、ベクトル '''''a''''' の成分 ''a{{sub|i}}''=('''''e'''{{sub|i}}'','''''a''''') により列ベクトルとの同一視 |
||
{{Indent| |
{{Indent| |
||
| 72行目: | 151行目: | ||
<math>[\boldsymbol{a}, \boldsymbol{b}]_i=\sum_{j,k}\epsilon_{ijk} a_j b_k</math> |
<math>[\boldsymbol{a}, \boldsymbol{b}]_i=\sum_{j,k}\epsilon_{ijk} a_j b_k</math> |
||
}} |
}} |
||
である。 |
|||
== クロス積の幾何的意味 == |
|||
[[ファイル:Cross_product_parallelogram.svg|右|サムネイル|(図1)2つのベクトルのクロス積の大きさは、それらが作る[[平行四辺形]]の大きさとなる。]] |
|||
[[ファイル:Parallelepiped_volume.svg|右|サムネイル|240x240ピクセル|(図2)3つのベクトルのクロス積は、[[平行六面体]]を定義する。]] |
|||
2つのベクトルのクロス積は、2つのベクトルが作る[[平行四辺形]]の大きさに等しい(図1)。 |
|||
<math display="block"> \left\| \boldsymbol{a} \times \boldsymbol{b} \right\| = \left\| \boldsymbol{a} \right\| \left\| \boldsymbol{b} \right\| \left| \sin \theta \right| </math> |
|||
また、3つのベクトル '''''a'''''、'''''b'''''、'''''c'''''は、[[平行六面体]]を定義する。(図2)。この[[平行六面体]]の体積 ''V''について、 |
|||
<math>V = |\boldsymbol{a} \cdot (\boldsymbol{b} \times \boldsymbol{c})|</math> |
|||
が成り立つ。ここで絶対値記号を付けたのは、3つのベクトルのクロス積が負になる場合を考慮してのことである。 |
|||
なお、 |
|||
<math> |
|||
\boldsymbol{a}\cdot(\boldsymbol{b}\times \boldsymbol{c})= |
|||
\boldsymbol{b}\cdot(\boldsymbol{c}\times \boldsymbol{a})= |
|||
\boldsymbol{c}\cdot(\boldsymbol{a}\times \boldsymbol{b}) |
|||
</math> |
|||
である。 |
である。 |
||
== 性質 == |
== 性質 == |
||
=== 双線型性 === |
|||
行列式の[[線型性#重線型|多重線型性]]から、ベクトル積も[[線型性#重線型|双線型性]]である。任意のベクトルに '''''a'''''、'''''b'''''、'''''c''''' とスカラー ''k''、''l'' に対して |
|||
{{Indent| |
|||
<math>[\boldsymbol{a},k\boldsymbol{b}+l\boldsymbol{c}] =k[\boldsymbol{a},\boldsymbol{b}] +l[\boldsymbol{a},\boldsymbol{c}]</math> |
|||
}} |
|||
{{Indent| |
|||
<math>[k\boldsymbol{b}+l\boldsymbol{c},\boldsymbol{a}] =k[\boldsymbol{b},\boldsymbol{a}] +l[\boldsymbol{c},\boldsymbol{a}]</math> |
|||
}} |
|||
が成り立つ。特に ''k''=''l''=0 であれば |
|||
{{Indent| |
|||
<math>[\boldsymbol{a},\boldsymbol{0}] |
|||
=[\boldsymbol{0}, \boldsymbol{a}] =\boldsymbol{0}</math> |
|||
}} |
|||
である。内積(スカラー積)の場合は[[零ベクトル]]との積はスカラーのゼロであるが、ベクトル積の場合は零ベクトルであることに注意が必要。 |
|||
=== |
=== 分配律 === |
||
一般に[[分配律]] |
|||
行列式の交代性から、ベクトル積も交代性をもつ。任意のベクトル '''''a'''''、'''''b''''' に対して |
|||
{{Indent| |
|||
* {{math|'''a''' × ('''b''' + '''c''') {{=}} '''a''' × '''b''' + '''a''' × '''c'''}} (角括弧表記では{{math|1=['''a''', '''b+c'''] = ['''a''', '''b'''] + ['''a''', '''c''']}}) |
|||
<math>[\boldsymbol{b}, \boldsymbol{a}] = -[\boldsymbol{a}, \boldsymbol{b}]</math> |
|||
が成り立つ。 |
|||
}} |
|||
が成り立つ。特に、自分自身とのベクトル積は |
|||
=== 反交換律 === |
|||
{{Indent| |
|||
一般に[[反交換律]] |
|||
* {{math|'''a''' × '''b''' {{=}} − '''b''' × '''a'''}} (角括弧表記では{{math|1=['''b''', '''a'''] = -['''a''', '''b''']}}) |
|||
が成り立つ。これは、[[行列式]]の交代性や[[リー代数]]の[[反交換性]]からも説明できる。特に、自分自身とのベクトル積は{{Indent| |
|||
<math>[\boldsymbol{a}, \boldsymbol{a}] = \boldsymbol{0}</math> |
<math>[\boldsymbol{a}, \boldsymbol{a}] = \boldsymbol{0}</math> |
||
}} |
}} |
||
であり恒等的に零ベクトルである。(複零性) |
であり恒等的に零ベクトルである。(複零性) |
||
内積の性質 |
内積の性質、 |
||
{{Indent| |
{{Indent| |
||
<math>(\boldsymbol{b}, \boldsymbol{a}) = (\boldsymbol{a}, \boldsymbol{b})</math> |
<math>(\boldsymbol{b}, \boldsymbol{a}) = (\boldsymbol{a}, \boldsymbol{b})</math> |
||
| 109行目: | 204行目: | ||
}} |
}} |
||
と異なることに注意が必要。 |
と異なることに注意が必要。 |
||
=== 双線型性 === |
|||
行列式の[[線型性#重線型|多重線型性]]から、ベクトル積も[[線型性#%E9%87%8D%E7%B7%9A%E5%9E%8B|双線型性]]である。任意のベクトルに '''''a'''''、'''''b'''''、'''''c''''' とスカラー ''k''、''l'' に対して |
|||
{{Indent|<math>[\boldsymbol{a},k\boldsymbol{b}+l\boldsymbol{c}] =k[\boldsymbol{a},\boldsymbol{b}] +l[\boldsymbol{a},\boldsymbol{c}]</math>}}{{Indent|<math>[k\boldsymbol{b}+l\boldsymbol{c},\boldsymbol{a}] =k[\boldsymbol{b},\boldsymbol{a}] +l[\boldsymbol{c},\boldsymbol{a}]</math>}} |
|||
が成り立つ。特に ''k''=''l''=0 であれば |
|||
{{Indent|<math>[\boldsymbol{a},\boldsymbol{0}] |
|||
=[\boldsymbol{0}, \boldsymbol{a}] =\boldsymbol{0}</math>}} |
|||
である。内積(スカラー積)の場合は[[零ベクトル]]との積はスカラーのゼロであるが、ベクトル積の場合は零ベクトルであることに注意が必要。 |
|||
=== ヤコビ恒等式 === |
=== ヤコビ恒等式 === |
||
| 161行目: | 264行目: | ||
ゆえに、 |
ゆえに、 |
||
: <math>\boldsymbol a \times (\boldsymbol b \times \boldsymbol c) = (\boldsymbol a \cdot \boldsymbol c) \boldsymbol b - (\boldsymbol a \cdot \boldsymbol b) \boldsymbol c</math> |
: <math>\boldsymbol a \times (\boldsymbol b \times \boldsymbol c) = (\boldsymbol a \cdot \boldsymbol c) \boldsymbol b - (\boldsymbol a \cdot \boldsymbol b) \boldsymbol c</math> |
||
== 図形的な理解 == |
|||
ベクトル積は幾何学的なベクトルに対する演算と解釈することで、図形的な理解が可能となる。 |
|||
行列式の交代性から |
|||
{{Indent| |
|||
<math>\boldsymbol{a} \cdot (\boldsymbol{a} \times \boldsymbol{b}) |
|||
=\boldsymbol{b} \cdot (\boldsymbol{a} \times \boldsymbol{b} )=0</math> |
|||
}} |
|||
である。 |
|||
従って、2つのベクトル '''''a'''''、'''''b''''' のベクトル積 '''''a'''''×'''''b''''' は、元のベクトル '''''a'''''、'''''b''''' の両方と直交する。言い換えれば、2つのベクトルが作る[[平面]]の[[法線]]と平行な方向を向いている。 |
|||
ただし、法線のどちらの方向に向いているかは座標軸の選び方に依存し、[[右手系]]と[[左手系]]に分けられる。右手系の場合は、'''''a''''' をその始点の周りに180度以下の回転角で回して '''''b''''' に重ねるときに右ねじの進む方向である。すなわち、右手の親指を '''''a'''''、人差し指を'''''b''''' としたときの中指がベクトル積 '''''a'''''×'''''b''''' の向きを表す。左手系の場合は、'''''b''''' をその始点の周りに180度以下の回転角で回して '''''a''''' に重ねるときに右ねじの進む向きである。 |
|||
行列式とスカラー積の線型性からベクトル積も双線型性をもつ。 |
|||
特に、2つのベクトル '''''a'''''、'''''b''''' のベクトル積 '''''a'''''×'''''b''''' は、元のベクトル '''''a'''''、'''''b''''' の大きさに比例する。 |
|||
また、二つのベクトル '''''a'''''、'''''b''''' のなす角を ''θ'' とすれば、標準的な基底の下で |
|||
{{Indent| |
|||
<math>\boldsymbol{a} = |
|||
\begin{pmatrix} |
|||
a \\ 0 \\ 0 \\ |
|||
\end{pmatrix},~ |
|||
\boldsymbol{b} = |
|||
\begin{pmatrix} |
|||
b\cos\theta \\ b\sin\theta \\ 0 \\ |
|||
\end{pmatrix}</math> |
|||
}} |
|||
と成分表示することができる。これらのベクトル積は |
|||
{{Indent| |
|||
<math>\boldsymbol{a} \times \boldsymbol{b} = |
|||
\begin{pmatrix} |
|||
0 \\ 0 \\ ab\sin\theta \\ |
|||
\end{pmatrix}</math> |
|||
}} |
|||
となる。従って、ベクトル積の大きさは |
|||
{{Indent| |
|||
<math>\vert \boldsymbol{a} \times \boldsymbol{b} \vert |
|||
=\vert \boldsymbol{a} \vert\, \vert \boldsymbol{b} \vert \sin\theta</math> |
|||
}} |
|||
であり、2つのベクトルが作る[[平行四辺形]]の面積に等しい。 |
|||
== 多次元への拡張 == |
== 多次元への拡張 == |
||
| 265行目: | 329行目: | ||
これら以外の次元では、必要な[[対称性]]を持つ乗算が定義できないため(これは[[アドルフ・フルヴィッツ]]によって証明された)、クロス積は定義できない。また、0次元では自明なことを確認できるにすぎず、1次元のクロス積は常に[[零ベクトル]]である。 |
これら以外の次元では、必要な[[対称性]]を持つ乗算が定義できないため(これは[[アドルフ・フルヴィッツ]]によって証明された)、クロス積は定義できない。また、0次元では自明なことを確認できるにすぎず、1次元のクロス積は常に[[零ベクトル]]である。 |
||
===直積を使った拡張(外積)=== |
=== 直積を使った拡張(外積) === |
||
クロス積は、直積 |
クロス積は、直積 |
||
:<math> \boldsymbol{a} \circ \boldsymbol{b} = \boldsymbol{a} \boldsymbol{b}^{\ |
:<math> \boldsymbol{a} \circ \boldsymbol{b} = \boldsymbol{a} \boldsymbol{b}^{\intercal} = (a_i b_j) </math> |
||
を使って |
を使って |
||
:<math> \boldsymbol a \times \boldsymbol b = \boldsymbol a \circ \boldsymbol b - \boldsymbol b \circ \boldsymbol a </math> (*) |
:<math> \boldsymbol a \times \boldsymbol b = \boldsymbol a \circ \boldsymbol b - \boldsymbol b \circ \boldsymbol a \quad</math> (*) |
||
と定義できる。ただしここで、[[反対称テンソル]]と[[擬ベクトル]]を等価 |
と定義できる。ただしここで、[[反対称テンソル]]と[[擬ベクトル]]を等価 |
||
:<math> (x, y, z) = \begin{pmatrix} 0 & z & -y \\ -z & 0 & x \\ y & -x & 0 \end{pmatrix} </math> |
:<math> (x, y, z) = \begin{pmatrix} 0 & z & -y \\ -z & 0 & x \\ y & -x & 0 \end{pmatrix} </math> |
||
としたが、これを[[ホッジ作用素]]で[[写像]]として明示すると |
としたが、これを[[ホッジ作用素]]<math>\star</math>で[[写像]]として明示すると |
||
:<math> \boldsymbol a \times \boldsymbol b = |
:<math> \boldsymbol a \times \boldsymbol b = \star ( \boldsymbol a \circ \boldsymbol b - \boldsymbol b \circ \boldsymbol a) </math> |
||
と書ける。 |
と書ける。 |
||
(*)式はそのまま、一般次元での定義に使える。ただし、これで定義できる積は、クロス積ではなく[[外積]]と呼び、 |
(*)式はそのまま、一般次元での定義に使える。ただし、これで定義できる積は、クロス積ではなく[[ウェッジ積|外積]]と呼び、 |
||
:<math> \boldsymbol a \wedge \boldsymbol b = \boldsymbol a \circ \boldsymbol b - \boldsymbol b \circ \boldsymbol a </math> |
:<math> \boldsymbol a \wedge \boldsymbol b = \boldsymbol a \circ \boldsymbol b - \boldsymbol b \circ \boldsymbol a </math> |
||
で表す。外積は3次元ではクロス積に一致するが、同義語ではないので注意が必要である。 |
で表す。外積は3次元ではクロス積に一致するが、同義語ではないので注意が必要である。 |
||
外積は2階の反対称テンソルであり、これはホッジ作用素により、''n'' 次元では ''n'' - 2 階の[[擬テンソル]]に写像できる。つまり、2次元では[[擬スカラー]](0階の擬テンソル)、3次元では[[擬ベクトル]](1階の擬テンソル)に写像できるが、4次元以上ではテンソルとして扱うしかない。 |
外積は2階の反対称テンソルであり、これはホッジ作用素により、''n'' 次元では ''n'' - 2 階の[[擬テンソル]]に写像できる。つまり、2次元では[[擬スカラー]](0階の擬テンソル)、3次元では[[擬ベクトル]](1階の擬テンソル)に写像できるが、4次元以上ではテンソルとして扱うしかない。 |
||
外積( |
外積({{Lang-de|äußeres Produkt}})は、[[ヘルマン・グラスマン|グラスマン]]によって導入されたが、当時はそれほど注目されず、彼の死後に高く評価された。 |
||
== 関連項目 == |
== 関連項目 == |
||
2024年2月25日 (日) 17:21時点における最新版

2つのベクトル a, b のクロス積は乗算記号を用いて a × b、あるいは角括弧を用いて [a, b] と表される。
呼称
[編集]「クロス積」という呼称は、積の記号に十字(×)を用いることに由来する(同様にベクトルの内積は点(⋅)を用いることからドット積と呼ばれる)。またクロス積の別称として、
日本語や中国語では、クロス積(叉積、叉积)をしばしば外積(外積、外积)と呼び、しばしば同義語として扱う。しかし「外積」という語は、より一般には外積代数における楔積も指し、必ずしも「クロス積」とは一致しない。 楔積とクロス積を区別のため、前者を外積と呼び後者をクロス積と呼ぶ。
outer product もまた「外積」と訳されるが、こちらは直積(direct product)を意味する。
表記
[編集]2つのベクトル a, b のクロス積は、以下のように表記される。
定義
[編集]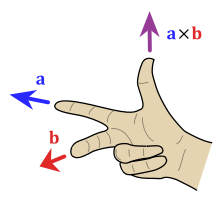

3次元空間上の2つのベクトル a, b のクロス積 a × b は、以下のように定義される:
ただし、θ は2つのベクトルのなす角の角度、|⋅| はベクトルの大きさ、n は2つのベクトルがなす平面に対し垂直な単位ベクトルを表す(n は右手系になるように取る)。
行列式による定義
[編集]3次元の向き付けられたベクトル空間におけるクロス積は、任意のベクトル v に対してドット積との間に
の関係を満たすベクトルの二項演算である。ここで ⟨ · , · , · ⟩ はベクトルを標準的な基底により列ベクトルと同一視することで得られる3次正方行列である。det は行列式を表す。
幾何的なベクトルの演算として定義できる。
行列式の交代性から、
である。
従って、2つのベクトル a、b のクロス積 a×b は、元のベクトル a、b の両方と直交する。言い換えれば、2つのベクトルが作る平面の法線と平行な方向を向いている。
ただし、法線のどちらの方向に向いているかは座標軸の選び方に依存し、右手系と左手系に分けられる。右手系の場合は、a をその始点の周りに180度以下の回転角で回して b に重ねるときに右ねじの進む方向である。すなわち、右手の親指を a、人差し指をb としたときの中指がクロス積 a×b の向きを表す。左手系の場合は、b をその始点の周りに180度以下の回転角で回して a に重ねるときに右ねじの進む向きである。
行列式とスカラー積の線型性からクロス積も双線型性をもつ。 特に、2つのベクトル a、b のクロス積 a×b は、元のベクトル a、b の大きさに比例する。 また、二つのベクトル a、b のなす角を θ とすれば、標準的な基底の下で
と成分表示することができる。これらのクロス積は
となる。従ってクロス積の大きさは
であり、2つのベクトルが作る平行四辺形の面積に等しい。
成分表示
[編集]標準的な基底を (ei,ej)=δi,j として、ベクトル a の成分 ai=(ei,a) により列ベクトルとの同一視
を行う。ベクトル a、b のベクトル積 [a,b] は
あるいは
となる。以上のことを形式的に
と表現することもある。
エディントンのイプシロン εijk を用いると
である。
クロス積の幾何的意味
[編集]

2つのベクトルのクロス積は、2つのベクトルが作る平行四辺形の大きさに等しい(図1)。
また、3つのベクトル a、b、cは、平行六面体を定義する。(図2)。この平行六面体の体積 Vについて、
が成り立つ。ここで絶対値記号を付けたのは、3つのベクトルのクロス積が負になる場合を考慮してのことである。
なお、
である。
性質
[編集]分配律
[編集]一般に分配律
- a × (b + c) = a × b + a × c (角括弧表記では[a, b+c] = [a, b] + [a, c])
が成り立つ。
反交換律
[編集]一般に反交換律
- a × b = − b × a (角括弧表記では[b, a] = -[a, b])
が成り立つ。これは、行列式の交代性やリー代数の反交換性からも説明できる。特に、自分自身とのベクトル積は
であり恒等的に零ベクトルである。(複零性)
内積の性質、
と異なることに注意が必要。
双線型性
[編集]行列式の多重線型性から、ベクトル積も双線型性である。任意のベクトルに a、b、c とスカラー k、l に対して
が成り立つ。特に k=l=0 であれば
である。内積(スカラー積)の場合は零ベクトルとの積はスカラーのゼロであるが、ベクトル積の場合は零ベクトルであることに注意が必要。
ヤコビ恒等式
[編集]ベクトル積による演算結果はベクトルなので、別のベクトルとのベクトル積を考えることができる。3つのベクトルのベクトル積はベクトル三重積と呼ばれている。ベクトル三重積は
となる。3つのスカラーの積と異なり、ベクトル三重積では一般に
であり、結合法則が成り立たない。ベクトル積では結合法則に代わって
の関係式が成り立つ。これを変形すれば
が得られ、ヤコビ恒等式と呼ばれている。
三重積の証明
[編集]ベクトル三重積:
ベクトルとベクトルの外積であるから、これはベクトルである。そのx 成分は
同様にして、y 成分、z 成分は、
ゆえに、
多次元への拡張
[編集]行列式を使った拡張
[編集]行列式による定義を拡張して、n 次元ベクトル空間における n - 1 項演算としてのベクトル積が
を定義できる。 完全反対称行列を用いれば
となる。
例えば、2次元のベクトル空間では単項演算として
となり、4次元ではそれぞれ三項演算として
となる。また、1次元では定数 1 となる。
多元数を使った拡張
[編集]3次元のクロス積
のベクトル成分で定義できる。ちなみに、スカラー成分を符号反転した は内積になっている。
3次元のクロス積はハミルトンの4元数の概念をもとにして、ウィラード・ギブズとオリヴァー・ヘヴィサイドがそれぞれ独立に、ドット積と対になる数学的概念として考案した。
これを多元数に拡張すると、n + 1 元数の乗算から n 次元でのクロス積を定義できる。つまり、実数(1元数)、複素数(2元数)、4元数、8元数の乗算から、0次元、1次元、3次元、7次元でのクロス積が定義できる(要素数が多くなるため縦ベクトルで表す)。
これら以外の次元では、必要な対称性を持つ乗算が定義できないため(これはアドルフ・フルヴィッツによって証明された)、クロス積は定義できない。また、0次元では自明なことを確認できるにすぎず、1次元のクロス積は常に零ベクトルである。
直積を使った拡張(外積)
[編集]クロス積は、直積
を使って
- (*)
と定義できる。ただしここで、反対称テンソルと擬ベクトルを等価
と書ける。
(*)式はそのまま、一般次元での定義に使える。ただし、これで定義できる積は、クロス積ではなく外積と呼び、
で表す。外積は3次元ではクロス積に一致するが、同義語ではないので注意が必要である。
外積は2階の反対称テンソルであり、これはホッジ作用素により、n 次元では n - 2 階の擬テンソルに写像できる。つまり、2次元では擬スカラー(0階の擬テンソル)、3次元では擬ベクトル(1階の擬テンソル)に写像できるが、4次元以上ではテンソルとして扱うしかない。
外積(ドイツ語: äußeres Produkt)は、グラスマンによって導入されたが、当時はそれほど注目されず、彼の死後に高く評価された。
関連項目
[編集]外部リンク
[編集]- 『外積』 - コトバンク
- 『ベクトル積』 - コトバンク
- Weisstein, Eric W. "Cross Product". mathworld.wolfram.com (英語).


![{\displaystyle [{\boldsymbol {a}},{\boldsymbol {b}}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b9312534b1ba4c99e32566a32c071977ddad384b)







![{\displaystyle [{\boldsymbol {a}},{\boldsymbol {b}}]_{1}=({\boldsymbol {e}}_{1},[{\boldsymbol {a}},{\boldsymbol {b}}])={\begin{vmatrix}1&a_{1}&b_{1}\\0&a_{2}&b_{2}\\0&a_{3}&b_{3}\\\end{vmatrix}}=a_{2}b_{3}-a_{3}b_{2}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4349b2fce366207e757ca54392f753a52fc9da0d)
![{\displaystyle [{\boldsymbol {a}},{\boldsymbol {b}}]_{2}=({\boldsymbol {e}}_{2},[{\boldsymbol {a}},{\boldsymbol {b}}])={\begin{vmatrix}0&a_{1}&b_{1}\\1&a_{2}&b_{2}\\0&a_{3}&b_{3}\\\end{vmatrix}}=a_{3}b_{1}-a_{1}b_{3}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e1511f42e28b2c8732131ea0bb027b684aa993e2)
![{\displaystyle [{\boldsymbol {a}},{\boldsymbol {b}}]_{3}=({\boldsymbol {e}}_{3},[{\boldsymbol {a}},{\boldsymbol {b}}])={\begin{vmatrix}0&a_{1}&b_{1}\\0&a_{2}&b_{2}\\1&a_{3}&b_{3}\\\end{vmatrix}}=a_{1}b_{2}-a_{2}b_{1}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f9f0207a5c8f10efb689e85cd510d213bb15f162)
![{\displaystyle [{\boldsymbol {a}},{\boldsymbol {b}}]\doteq {\begin{pmatrix}a_{2}b_{3}-a_{3}b_{2}\\a_{3}b_{1}-a_{1}b_{3}\\a_{1}b_{2}-a_{2}b_{1}\\\end{pmatrix}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/52d2a2643983ecdda9538f4b90fb3cc53f0423f4)
![{\displaystyle [{\boldsymbol {a}},{\boldsymbol {b}}]={\begin{vmatrix}{\boldsymbol {e}}_{1}&a_{1}&b_{1}\\{\boldsymbol {e}}_{2}&a_{2}&b_{2}\\{\boldsymbol {e}}_{3}&a_{3}&b_{3}\end{vmatrix}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9ecdc5222d6868cc91016a795adf8011d2b9f5bf)
![{\displaystyle [{\boldsymbol {a}},{\boldsymbol {b}}]_{i}=\sum _{j,k}\epsilon _{ijk}a_{j}b_{k}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f2e2b0ca64f606d305621506a8566769c3b6f6a6)



![{\displaystyle [{\boldsymbol {a}},{\boldsymbol {a}}]={\boldsymbol {0}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/de09f61713ceb571793a08c86640e65fca795744)


![{\displaystyle [{\boldsymbol {a}},k{\boldsymbol {b}}+l{\boldsymbol {c}}]=k[{\boldsymbol {a}},{\boldsymbol {b}}]+l[{\boldsymbol {a}},{\boldsymbol {c}}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e1a89fae470f1fdcdca0259bb3136f179e7982f0)
![{\displaystyle [k{\boldsymbol {b}}+l{\boldsymbol {c}},{\boldsymbol {a}}]=k[{\boldsymbol {b}},{\boldsymbol {a}}]+l[{\boldsymbol {c}},{\boldsymbol {a}}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b9c73e1f490b1534bc0d5a0dd98af0735a19ced7)
![{\displaystyle [{\boldsymbol {a}},{\boldsymbol {0}}]=[{\boldsymbol {0}},{\boldsymbol {a}}]={\boldsymbol {0}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/90fd83f7cab062ccbe03547df7ef0dbc69b29d75)
![{\displaystyle [{\boldsymbol {a}},[{\boldsymbol {b}},{\boldsymbol {c}}]]=({\boldsymbol {a}},{\boldsymbol {c}})\,{\boldsymbol {b}}-({\boldsymbol {a}},{\boldsymbol {b}})\,{\boldsymbol {c}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ac7503be70399904420db5aeeba3d86b227bd75c)
![{\displaystyle [{\boldsymbol {a}},[{\boldsymbol {b}},{\boldsymbol {c}}]]-[[{\boldsymbol {a}},{\boldsymbol {b}}],{\boldsymbol {c}}]\neq {\boldsymbol {0}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fe4ad1428e449a33b245c7890946b37a4bea4ca4)
![{\displaystyle [{\boldsymbol {a}},[{\boldsymbol {b}},{\boldsymbol {c}}]]-[[{\boldsymbol {a}},{\boldsymbol {b}}],{\boldsymbol {c}}]=[{\boldsymbol {b}},[{\boldsymbol {a}},{\boldsymbol {c}}]]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9e2a27c9dfd413efb3160594702c7b452389b76d)
![{\displaystyle [{\boldsymbol {a}},[{\boldsymbol {b}},{\boldsymbol {c}}]]+[{\boldsymbol {b}},[{\boldsymbol {c}},{\boldsymbol {a}}]]+[{\boldsymbol {c}},[{\boldsymbol {a}},{\boldsymbol {b}}]]={\boldsymbol {0}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/56d607faf2e8a034576fcf65d9632c1dc5c1853e)






![{\displaystyle ({\boldsymbol {v}},[{\boldsymbol {a}}_{1},\ldots ,{\boldsymbol {a}}_{n-1}])=\det \langle {\boldsymbol {v}},{\boldsymbol {a}}_{1},\ldots ,{\boldsymbol {a}}_{n-1}\rangle }](https://wikimedia.org/api/rest_v1/media/math/render/svg/5c7f2ed5805dda8d32ec655e9e7c00f0591e4be8)
![{\displaystyle [{\boldsymbol {a}}_{1},\ldots ,{\boldsymbol {a}}_{n-1}]_{i}=\sum _{j_{1},\ldots ,j_{n-1}}\epsilon _{i,j_{1},\ldots ,j_{n-1}}a_{1}^{j_{1}}\cdots a_{n-1}^{j_{n-1}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1849fb2030deceaab3a16064c64f671236ab5ec6)
![{\displaystyle [{\boldsymbol {a}}]={\begin{pmatrix}a_{2}\\-a_{1}\\\end{pmatrix}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ffd2fada44669d3c8511498290b506659f8e4891)
![{\displaystyle [{\boldsymbol {a}},{\boldsymbol {b}},{\boldsymbol {c}}]={\begin{pmatrix}+a_{2}b_{3}c_{4}+a_{3}b_{4}c_{2}+a_{4}b_{2}c_{3}-a_{2}b_{4}c_{3}-a_{3}b_{2}c_{4}-a_{4}b_{3}c_{2}\\-a_{3}b_{4}c_{1}-a_{4}b_{1}c_{3}-a_{1}b_{3}c_{4}+a_{3}b_{1}c_{4}+a_{4}b_{3}c_{1}+a_{1}b_{4}c_{3}\\+a_{4}b_{1}c_{2}+a_{1}b_{2}c_{4}+a_{2}b_{4}c_{1}-a_{4}b_{2}c_{1}-a_{1}b_{4}c_{2}-a_{2}b_{1}c_{4}\\-a_{1}b_{2}c_{3}-a_{2}b_{3}c_{1}-a_{3}b_{1}c_{2}+a_{1}b_{3}c_{2}+a_{2}b_{1}c_{3}+a_{3}b_{2}c_{1}\\\end{pmatrix}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e21e567381f509202aa3e7ffd6841c1297e8f9e0)











