Abstract
We investigate heat-pumped single-mode amplifiers of quantized fields in high-Q cavities based on noninverted two-level systems. Their power generation is shown to crucially depend on the capacity of the quantum state of the field to accumulate useful work. By contrast, the energy gain of the field is shown to be insensitive to its quantum state. Analogies and differences with masers are explored.
Export citation and abstract BibTeX RIS
Einführung
Thermodynamics divides the energy interchanged between systems and their surrounding ("baths") into heat and work in an asymmetric fashion: While work can be entirely transformed into heat in a cyclic process, the opposite is not true [1]: the energy exchanged by a system in a closed cycle is divided between work, W, and heat, Q. For a quantum system the accepted division is given by [2–4]
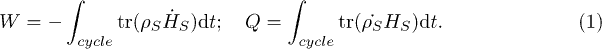
Both W and Q are determined by the parametrically (classically) driven Hamiltonian  and by
and by 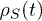 , the reduced density matrix of the system S. Positive W stands for work done in a cycle by S. Equation (1) underlies the numerous quantum heat engine (QHE) models that have been proposed to date [2-19]. These models may be deemed semiclassical, as they employ classical fields or forces that drive quantum systems [20]. In these models the cycle usually consists of "strokes" (legs) in which the system ("working fluid"), S, alternates between coupling to the "hot" (H) and "cold" (C) heat baths.
, the reduced density matrix of the system S. Positive W stands for work done in a cycle by S. Equation (1) underlies the numerous quantum heat engine (QHE) models that have been proposed to date [2-19]. These models may be deemed semiclassical, as they employ classical fields or forces that drive quantum systems [20]. In these models the cycle usually consists of "strokes" (legs) in which the system ("working fluid"), S, alternates between coupling to the "hot" (H) and "cold" (C) heat baths.
We have recently [21,22] put forward a minimal semiclassical QHE model whose "working fluid" consists of a two-level system (TLS) that is permanently coupled to spectrally separated H and C baths and is governed by
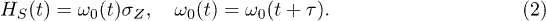
Here  is the population-difference operator and τ is the period of the parametric modulation (Stark-shift) effected, e.g., by an off-resonant classical field with sinusoidal amplitude
is the population-difference operator and τ is the period of the parametric modulation (Stark-shift) effected, e.g., by an off-resonant classical field with sinusoidal amplitude  : the modulating field plays the role of a "piston" (P). This nonadiabatic model circumvents the problem of breaking a finite-time cycle into strokes: the commonly assumed abrupt on-off switching of system-bath interactions in separate strokes of such nonadiabatic cycles may strongly affect their energy and entropy exchange and thereby their quantum state, which casts doubts on the validity of existing models of finite-time engines, as they ignore such effects.
: the modulating field plays the role of a "piston" (P). This nonadiabatic model circumvents the problem of breaking a finite-time cycle into strokes: the commonly assumed abrupt on-off switching of system-bath interactions in separate strokes of such nonadiabatic cycles may strongly affect their energy and entropy exchange and thereby their quantum state, which casts doubts on the validity of existing models of finite-time engines, as they ignore such effects.
Yet what if we wish to analyze the performance of fully quantized (rather than semiclassical) engines [23]? Namely, what if we wish to examine the power generation in a QHE upon preparing the initial quantum state of the piston (field) P, then coupling P to the system S and letting S+P evolve under the time-independent Hamiltonian  along with the permanent action of the baths H and C? Such scenarios may arise in opto-mechanical and nano-mechanical setups [24,25] or in cavity-field amplifiers (masers) [20,26]. Understanding such scenarios is not only important for applied purposes but is a necessary step towards clarifying the fundamental question: is thermodynamic performance different for quantum and classical or semiclassical devices? Here we explore this question for QHEs, by asking specifically: a) What is the proper definition of work when the standard formula (eq. (1)) does not apply, since P affects S via a time-independent Hamiltonian? To this end, we invoke a seldom-used but rigorous definition of work in fully quantized setups [27,28]. b) Is work extraction sensitive to the quantum state of P, and is work distinguishable from energy exchange in a QHE? We investigate this virtually unexplored issue in a quantized analog of the semiclassical minimal model described by eq. (2), i.e., to a heat-pumped cavity-field amplifier and compare it to its known maser predecessors [20,26]. Work fluctuations [29] will be considered elsewhere.
along with the permanent action of the baths H and C? Such scenarios may arise in opto-mechanical and nano-mechanical setups [24,25] or in cavity-field amplifiers (masers) [20,26]. Understanding such scenarios is not only important for applied purposes but is a necessary step towards clarifying the fundamental question: is thermodynamic performance different for quantum and classical or semiclassical devices? Here we explore this question for QHEs, by asking specifically: a) What is the proper definition of work when the standard formula (eq. (1)) does not apply, since P affects S via a time-independent Hamiltonian? To this end, we invoke a seldom-used but rigorous definition of work in fully quantized setups [27,28]. b) Is work extraction sensitive to the quantum state of P, and is work distinguishable from energy exchange in a QHE? We investigate this virtually unexplored issue in a quantized analog of the semiclassical minimal model described by eq. (2), i.e., to a heat-pumped cavity-field amplifier and compare it to its known maser predecessors [20,26]. Work fluctuations [29] will be considered elsewhere.
Work in fully quantized setups
Work extraction from a QHE is governed by a nonunitary Liouville equation, which accounts for the indirect interaction of P with the baths, mediated by S. One may be tempted to exclude S and consider P as the working fluid, but such a QHE would not be autonomous, i.e., it would require external parametric driving. What determines the maximum work extractable by P from the baths via S? If P could unitarily evolve from its state  to another state, then the energy difference between the two states would be purely work, without entropy or heat change. Hence, for a given
to another state, then the energy difference between the two states would be purely work, without entropy or heat change. Hence, for a given  the maximum extractable work is
the maximum extractable work is
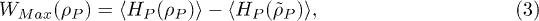
where  is a unitarily accessible state (i.e. a state with the same entropy as
is a unitarily accessible state (i.e. a state with the same entropy as 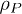 ) that minimizes the mean energy of P,
) that minimizes the mean energy of P,  (and thus maximizes the work extraction), known as a passive state [27,28]. By this definition, for passive states
(and thus maximizes the work extraction), known as a passive state [27,28]. By this definition, for passive states  (no extractable work).
(no extractable work).
The upper bound on  is obtained by minimizing the second term on the r.h.s. of eq. (3). This would ideally require a unitary transformation of
is obtained by minimizing the second term on the r.h.s. of eq. (3). This would ideally require a unitary transformation of  such that
such that  , since the passive Gibbs state is the minimal-energy state with the same entropy as
, since the passive Gibbs state is the minimal-energy state with the same entropy as  and a real temperature
and a real temperature  , where Z is a normalizing factor. Yet such a unitary process typically does not exist. We therefore extend the definition [27,28] in (3) as follows: we parametrize the unitarily (or iso-entropically) accessible
, where Z is a normalizing factor. Yet such a unitary process typically does not exist. We therefore extend the definition [27,28] in (3) as follows: we parametrize the unitarily (or iso-entropically) accessible  with the least
with the least 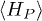 as if it were a Gibbs state, i.e. TP is defined as an effective temperature.
as if it were a Gibbs state, i.e. TP is defined as an effective temperature.
Equation (3) may be adapted to nonunitary engine action: as the initial piston state  evolves to a new state
evolves to a new state  , the corresponding change of the maximum extractable work can be expressed as
, the corresponding change of the maximum extractable work can be expressed as 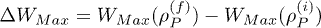 , since eq. (3) defines WMax for each state, and may be used to infer
, since eq. (3) defines WMax for each state, and may be used to infer  as
as 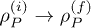 . Upon taking the time derivative of this bound, we find that the extractable power in a nonpassive state of P has the upper bound
. Upon taking the time derivative of this bound, we find that the extractable power in a nonpassive state of P has the upper bound
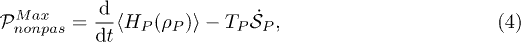
where we have used the fact that the entropy rate of change of the effective Gibbs state satisfies  .
.
To compare this bound on power to its semiclassical counterpart, we may invoke the first law of thermodynamics (energy conservation) for the total (closed) complex of S, P, cold (C) and hot (H) baths. In doing so we assume that S has reached the steady state, so that 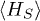 and the entropy of S have become constant. The standard expression for power generated by the QHE (also known as the canonical expression) has then the form [3]
and the entropy of S have become constant. The standard expression for power generated by the QHE (also known as the canonical expression) has then the form [3]

where the heat currents 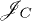 and
and 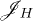 express the energy flow between the respective baths and S [3,7,21,22]. Equation (5) follows from the first law of thermodynamics, but the customary identification of the engine power with
express the energy flow between the respective baths and S [3,7,21,22]. Equation (5) follows from the first law of thermodynamics, but the customary identification of the engine power with  may be untrue: such identification ignores the entropy change of P with time, which may only be justified if P is a classical field. Consequently, the use of
may be untrue: such identification ignores the entropy change of P with time, which may only be justified if P is a classical field. Consequently, the use of  fails to distinguish between work and heat production in the quantum limit, as opposed to eq. (4).
fails to distinguish between work and heat production in the quantum limit, as opposed to eq. (4).
Fig. 1. (Colour on-line) Upper panel: a superconducting flux qubit S coupled to baths H,C. The piston P is a mechanical oscillator (cantilever) whose position affects Φ and thereby the energy of S. P has the capacity to do mechanical work on the external oscillator X. Middle panel: analogous setup, where P is a coplanar-resonator mode, whose magnetic field contributes to the flux Φ through the qubit. Here P has the capacity to do electromagnetic work on LC-circuit X. Lower panel: energy gain (dashed line) and work-capacity bound (solid line) for an initial (a) Fock state, (b) coherent state, in the gain regime  (energy arbitrary units, cycles
(energy arbitrary units, cycles ). (c) For
). (c) For 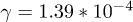 (loss regime) or single bath, the coherent-state work capacity decreases rapidly while the energy decreases slowly. The value of γ does not affect the bound but work extraction demands
(loss regime) or single bath, the coherent-state work capacity decreases rapidly while the energy decreases slowly. The value of γ does not affect the bound but work extraction demands 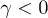 .
.
Download figure:
Standard imageWhat is required for an increase in the maximum extractable work WMax as the QHE evolves, i.e., for 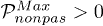 ? We find that the necessary (but not sufficient) condition is that the initial state
? We find that the necessary (but not sufficient) condition is that the initial state 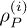 must be nonpassive, since (dissipative or amplifying) evolution may not change a passive state to a nonpassive one, at least under the standard Markovian assumption (see below). By contrast, a nonpassive P state under such evolution may yield
must be nonpassive, since (dissipative or amplifying) evolution may not change a passive state to a nonpassive one, at least under the standard Markovian assumption (see below). By contrast, a nonpassive P state under such evolution may yield 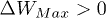 , i.e., it allows potential work accumulation in P. This accumulation (capacity) can be turned into real (extracted) work if and when P is coupled to an external degree of freedom (X); e.g., a piston in an opto-(or nano)-mechanical setup [24,25] can be coupled to an external cantilever (fig. 1, upper panel). The amount of extracted work will depend on the X-P coupling, but the capacity can be evaluated independently of this coupling.
, i.e., it allows potential work accumulation in P. This accumulation (capacity) can be turned into real (extracted) work if and when P is coupled to an external degree of freedom (X); e.g., a piston in an opto-(or nano)-mechanical setup [24,25] can be coupled to an external cantilever (fig. 1, upper panel). The amount of extracted work will depend on the X-P coupling, but the capacity can be evaluated independently of this coupling.
Cavity-based heat-pumped amplifier
The implications of the general work and power analysis presented above will be elucidated for the simplest (minimal) model of an autonomous QHE: a harmonic-oscillator P (the simplest unbounded-energy piston) that acts dispersively on a qubit S (i.e. without changing its level populations), while S is permanently coupled to baths H, C. This quantized analog of the semiclassical model of eq. (2) [21] will be shown to allow heat-pumped amplification of P via non-inverted S. At the heart of this model is the off-resonant coupling of P to the 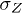 operator of S:
operator of S:

where g is the coupling strength and a and 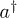 are, respectively, the P-mode annihilation and creation operators. This coupling is realizable, e.g., in the dispersive regime of a superconducting qubit in a resonator (see below) (fig. 1, middle panel) [24,30].
are, respectively, the P-mode annihilation and creation operators. This coupling is realizable, e.g., in the dispersive regime of a superconducting qubit in a resonator (see below) (fig. 1, middle panel) [24,30].
The engine is fueled by the H bath. The system-bath (S-B) coupling has the spin-boson form 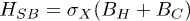 where
where 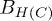 are the multimode bath operators. Namely, the dipolar
are the multimode bath operators. Namely, the dipolar 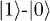 transition between the qubit states couples to two mode-continua at different temperatures. Under the bath-induced dynamics for the S+P state,
transition between the qubit states couples to two mode-continua at different temperatures. Under the bath-induced dynamics for the S+P state, 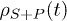 , S reaches the steady state while P still slowly gains (or loses) energy and work over many cycles. From the reduced density matrix of the piston
, S reaches the steady state while P still slowly gains (or loses) energy and work over many cycles. From the reduced density matrix of the piston 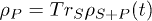 we can then compute the heat currents, the entropy
we can then compute the heat currents, the entropy  and the effective temperature TP in eq. (4), to find the conditions for sustainable QHE operation. In this analysis we wish to ensure that the second law is satisfied. We therefore subscribe to the common description [2-23] of the bath-induced dynamics by the Lindblad (or, more correctly, the Lindblad-Gorini-Kossakowski-Sudarshan (LGKS) generator which adheres to the second law [31].
and the effective temperature TP in eq. (4), to find the conditions for sustainable QHE operation. In this analysis we wish to ensure that the second law is satisfied. We therefore subscribe to the common description [2-23] of the bath-induced dynamics by the Lindblad (or, more correctly, the Lindblad-Gorini-Kossakowski-Sudarshan (LGKS) generator which adheres to the second law [31].
In the dressed-state basis that diagonalizes the S+P Hamiltonian
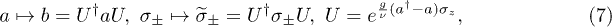
the Lindblad generator involves the bath response at the Hamiltonian eigenvalues: the resonant qubit (S) frequency  and the combination frequencies
and the combination frequencies 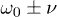 , ν being the piston (P) frequency. Namely
, ν being the piston (P) frequency. Namely
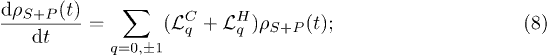
where 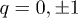 labels
labels  of S+P, and the generators associated with harmonic qν in the two baths are
of S+P, and the generators associated with harmonic qν in the two baths are 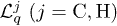 . These generators have the following form for the weak S-P coupling,
. These generators have the following form for the weak S-P coupling,  :
:
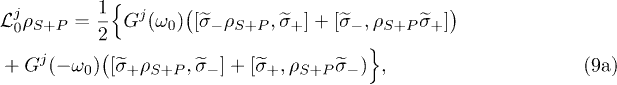
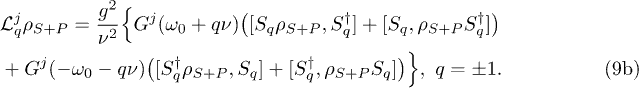
 , by
, by 
The transition operators 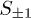 describe the relaxation of S accompanied by the respective excitation or deexcitation of P, while
describe the relaxation of S accompanied by the respective excitation or deexcitation of P, while  describe their time-reversed counterparts. The effects of the baths in eqs. (8), (9b) are here described by the Fourier transforms of the autocorrelation functions
describe their time-reversed counterparts. The effects of the baths in eqs. (8), (9b) are here described by the Fourier transforms of the autocorrelation functions  .
.
Work extraction from a given state
To evaluate the state dependence of work in this model we cast the (master) equation for 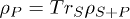 (obtained from eqs. (8), (9)) into a Fokker-Planck (FP) equation [20,32,33] for the phase-space (quasiprobability) distribution in the coherent-state basis,
(obtained from eqs. (8), (9)) into a Fokker-Planck (FP) equation [20,32,33] for the phase-space (quasiprobability) distribution in the coherent-state basis,  . Upon assuming a steady state for S and using standard methods [20,32], we derive the FP equation
. Upon assuming a steady state for S and using standard methods [20,32], we derive the FP equation
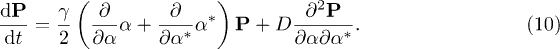
Here the drift and diffusion coefficients, γ and D, respectively, depend on 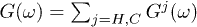 , which is the sum of the cold- and hot-baths response spectra, sampled at
, which is the sum of the cold- and hot-baths response spectra, sampled at  . These coefficients read
. These coefficients read
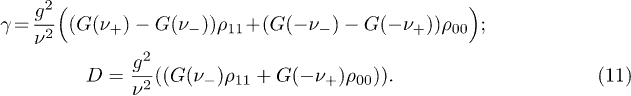
Their significance becomes apparent when the piston mean energy (for gain or loss) is evaluated to be
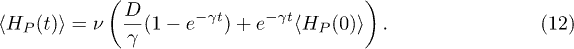
This mean energy is independent of the nonpassivity of the initial state, but is dependent on the drift of the initial energy (second r.h.s. term) countered by diffusion (first r.h.s. term). Energy gain occurs for 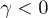 . It may be interpreted as heat pumping of P via absorption of quanta by the TLS from the H bath at
. It may be interpreted as heat pumping of P via absorption of quanta by the TLS from the H bath at  and their emission to the C bath at
and their emission to the C bath at  (fig. 2(a)), endowing P with the energy
(fig. 2(a)), endowing P with the energy  . Weak diffusion and high gain,
. Weak diffusion and high gain,  and
and  , require that the two response spectra,
, require that the two response spectra,  and
and  be separated (fig. 2(a)), just as in the semiclassical limit (2) [21].
be separated (fig. 2(a)), just as in the semiclassical limit (2) [21].
The heat-pumped energy in eq. (12) may be partly converted into work accumulated by P, measured by  : the work-capacity increase by the evolving non passivity of the phase-space distribution, as
: the work-capacity increase by the evolving non passivity of the phase-space distribution, as 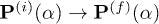 , under the FP equation dynamics. We ask: what determines whether a state is nonpassive and suited for work extraction? To this end we look for criteria for sustainable nonpassivity. This requires non-monotonic decrease of
, under the FP equation dynamics. We ask: what determines whether a state is nonpassive and suited for work extraction? To this end we look for criteria for sustainable nonpassivity. This requires non-monotonic decrease of  with the energy
with the energy 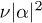 at long times. This requirement may be formulated as follows: nonpassivity requires positive derivative of
at long times. This requirement may be formulated as follows: nonpassivity requires positive derivative of 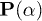 with respect to
with respect to  . We may use this requirement to classify work extraction by the quantum state of P, upon noting that the main contribution to the derivative comes from
. We may use this requirement to classify work extraction by the quantum state of P, upon noting that the main contribution to the derivative comes from 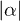 close to the center of the distribution (fig. 2(b)): a) An initially passive (e.g., thermal) state will only have negative derivative, i.e., will remain passive at all times, with no work extraction at any time. b) Only
close to the center of the distribution (fig. 2(b)): a) An initially passive (e.g., thermal) state will only have negative derivative, i.e., will remain passive at all times, with no work extraction at any time. b) Only 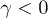 can yield sustainable work, since for
can yield sustainable work, since for 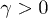 (loss regime) the distribution becomes eventually thermal (fig. 1(c)). c) Since in a Fock state the center of
(loss regime) the distribution becomes eventually thermal (fig. 1(c)). c) Since in a Fock state the center of 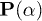 is at the origin
is at the origin  it can be shown that the derivative eventually becomes negative and the distribution passive for any γ. Thus, a Fock state gradually loses all its nonpassivity and work capacity. The work that may be extracted from an initial photon-number (Fock) state
it can be shown that the derivative eventually becomes negative and the distribution passive for any γ. Thus, a Fock state gradually loses all its nonpassivity and work capacity. The work that may be extracted from an initial photon-number (Fock) state 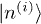 is at most its initial energy
is at most its initial energy  : a Fock state cannot extract additional work from the bath-fueled engine, hence its
: a Fock state cannot extract additional work from the bath-fueled engine, hence its  (fig. 1(a)). d) By contrast, in a coherent state, whose distribution is centered at
(fig. 1(a)). d) By contrast, in a coherent state, whose distribution is centered at  the derivative remains positive and the state can be shown to increase its nonpassivity for
the derivative remains positive and the state can be shown to increase its nonpassivity for 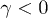 , so that work extraction is sustainable at all times. Maximal work capacity is then described by a displacement (following the engine action) of the final distribution,
, so that work extraction is sustainable at all times. Maximal work capacity is then described by a displacement (following the engine action) of the final distribution,  , to
, to 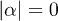 . This displacement operation is the unitary in eq. (3) that transforms
. This displacement operation is the unitary in eq. (3) that transforms  to
to 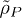 . The coherent-state capacity exponentially increases under negative
. The coherent-state capacity exponentially increases under negative  (figs. 1(b), 2(b)).
(figs. 1(b), 2(b)).
Fig. 2. (Colour on-line) (a) S-B coupling spectra and level scheme. (b) Phase-plane distributions (for 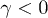 ): initial Fock state (left), coherent state (right) at t = 0 (above); after 104 cycles (below) (same parameters as in fig. 1. The Fock-state distribution becomes passive (thermalizes) but the coherent-state distribution increases its nonpassivity.
): initial Fock state (left), coherent state (right) at t = 0 (above); after 104 cycles (below) (same parameters as in fig. 1. The Fock-state distribution becomes passive (thermalizes) but the coherent-state distribution increases its nonpassivity.
Download figure:
Standard imageFor a piston in an initial passive state (or even in a Fock state), the engine needs an "ignition", which can be achieved by coherence injection:  , where
, where  is the displacement operator [20] and
is the displacement operator [20] and 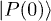 is the initial piston state.
is the initial piston state.
The fact that eq. (12) allows the amplification of the mean energy 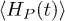 for any initial state, even for thermal input in P is consistent with
for any initial state, even for thermal input in P is consistent with 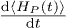 being the power generated according to the canonical definition (5): Clearly, such amplified thermal field contributes to heat rather than work. Hence, the canonical definition, as opposed to eq. (4), does not distinguish work from heat generation. We have thus reached the main conclusion of this paper: the extractable work obtainable from the nonpassivity equation (4) strongly depends on the initial state of the piston, but particularly on its coherence, rather than purity.
being the power generated according to the canonical definition (5): Clearly, such amplified thermal field contributes to heat rather than work. Hence, the canonical definition, as opposed to eq. (4), does not distinguish work from heat generation. We have thus reached the main conclusion of this paper: the extractable work obtainable from the nonpassivity equation (4) strongly depends on the initial state of the piston, but particularly on its coherence, rather than purity.
Experimental predictions
The S-P coupling in eq. (6) is realizable in well-investigated experimental setups [24,25]: 1) A superconducting flux qubit which is dispersively coupled to P may be realized by a high-Q (phonon) mode of a nano-mechanical cavity (cantilever). The quantized position of P, 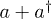 , affects the magnetic flux Φ through the qubit and thereby its frequency
, affects the magnetic flux Φ through the qubit and thereby its frequency  (fig. 1, upper panel). 2) Alternatively, P can be a field mode of a coplanar resonator [30] whose quantized electromagnetic field position
(fig. 1, upper panel). 2) Alternatively, P can be a field mode of a coplanar resonator [30] whose quantized electromagnetic field position 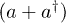 affects the flux Φ. In both setups, the coupling of the qubit to a bath at TH with a spectrum centered at
affects the flux Φ. In both setups, the coupling of the qubit to a bath at TH with a spectrum centered at 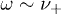 is achievable by a narrow-band local heat-pump, along with its coupling to a heat-dump at TC with a spectrum limited to
is achievable by a narrow-band local heat-pump, along with its coupling to a heat-dump at TC with a spectrum limited to  (fig. 2(a)). A drift
(fig. 2(a)). A drift 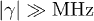 is feasible. In such scenarios, it should be possible to achieve
is feasible. In such scenarios, it should be possible to achieve 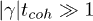 where
where 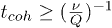 is the P-mode coherence time, and thus coherently amplify the output signal. Similar considerations may apply to cold-atom [34] or spin-ensembles [35] in high-Q cavities.
is the P-mode coherence time, and thus coherently amplify the output signal. Similar considerations may apply to cold-atom [34] or spin-ensembles [35] in high-Q cavities.
The protocol starts by preparing the qubit in the 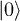 state, and concurrently preparing the piston-mode in a chosen initial state (thermal, coherent or Fock state) by established techniques [20,32]. Next, the dispersive S-P coupling (eq. (6)) is switched on by tuning their frequencies. The main signature of the predicted effects is the dependence of work on the initial state of P, for a given γ, as opposed to the energy gain of the P mode (eq. (12)) that should be independent of the initial state. Energy gain can be measured by resonant absorption at frequency ν of phonons (fig. 1, upper panel) or photons (fig. 1, middle panel). Measuring the work capacity (fig. 1(a), (b)) is more subtle. We may multiplex (homodyne) the P-mode field with a local oscillator [20,32]: only the coherent component of the P-mode field will then contribute to the output signal and to work, in contrast to the total energy gain which is insensitive to the coherence.
state, and concurrently preparing the piston-mode in a chosen initial state (thermal, coherent or Fock state) by established techniques [20,32]. Next, the dispersive S-P coupling (eq. (6)) is switched on by tuning their frequencies. The main signature of the predicted effects is the dependence of work on the initial state of P, for a given γ, as opposed to the energy gain of the P mode (eq. (12)) that should be independent of the initial state. Energy gain can be measured by resonant absorption at frequency ν of phonons (fig. 1, upper panel) or photons (fig. 1, middle panel). Measuring the work capacity (fig. 1(a), (b)) is more subtle. We may multiplex (homodyne) the P-mode field with a local oscillator [20,32]: only the coherent component of the P-mode field will then contribute to the output signal and to work, in contrast to the total energy gain which is insensitive to the coherence.
It is instructive to compare the present model with the micromaser model [20] in which the bath is at zero temperature and the gain depends on the interaction parameter  , where g is the coupling between the inverted atoms and the cavity-field mode,
, where g is the coupling between the inverted atoms and the cavity-field mode,  is the cavity mean photon number and τ is the time the atoms spend in the cavity. If the interaction parameter is assumed small, then from ref. [20] we obtain the generated power
is the cavity mean photon number and τ is the time the atoms spend in the cavity. If the interaction parameter is assumed small, then from ref. [20] we obtain the generated power  . Here
. Here 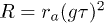 , where ra is the rate at which the atoms enter to the cavity. The generated power in this case is
, where ra is the rate at which the atoms enter to the cavity. The generated power in this case is  . The invested (input) power, the energy given by the inverted atoms to the field mode, is
. The invested (input) power, the energy given by the inverted atoms to the field mode, is  . We then obtain the maximum efficiency
. We then obtain the maximum efficiency 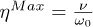 , i.e., the ratio between the output and input frequency. In our model, where atoms are noninverted, the analogous efficiency bound is
, i.e., the ratio between the output and input frequency. In our model, where atoms are noninverted, the analogous efficiency bound is  . It is obtained from the ratio of the power output to the input heat-power JH, for
. It is obtained from the ratio of the power output to the input heat-power JH, for  , the semiclassical limit for coherent-state input.
, the semiclassical limit for coherent-state input.
Conclusions
QHE performance, achievable at long but finite times [2–4,7,16,17,36] upon allowing for the piston quantum state to change its entropy, is both a practically and conceptually important issue, here studied for piston amplification under steady-state conditions for the working fluid. Our results elucidate the rapport between heat engine thermodynamics and its hitherto unfamiliar quantum properties. Namely, work extraction in the quantum domain is described as deviation from a passive state. This description, extended by us to nonunitary amplification of the piston (QHE evolution), correctly divides the energy exchange into work and heat in a fully quantized setup, by treating the piston as a thermodynamic resource with effective temperature and entropy. Remarkably, work extraction defined by nonpassivity crucially depends on the initial quantum state, in contrast to energy gain that adheres to the canonical definition, which fails to distinguish work from heat production (see also [37]). The most striking result is that coherence rather than purity of the quantum state determines work extraction, as manifested by the drastic difference between Fock- and coherent-state input. Further research may strive to encompass the present scenario with that of coherence in multilevel systems [36,38], entanglement in multiatom systems [39–44] and non-Markovian effects [45–49] in the general framework of nonclassical heat engines.
Acknowledgments
The support of ISF and BSF (GK), MNiSW (RA) and CONACYT (DG-K) is acknowledged.







